1. 两个栈实现一个队列:[^本题考点 队列 栈]
队列
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
对列的添加 insert append
队列的取值 列表[-1] 列表[0]
队列的删除 pop() pop(0)
栈
栈(stack)又名堆栈,它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
只允许在栈的栈顶来操作。
添加元素用append(push),称作是进栈,入栈或者压栈
取值列表[-1],因为它只能从栈顶来取值,相当于取列表的最后一个值,所以用索引-1.
删除元素pop()从后端开始删除。称作是出栈或者退栈。
1. 两个栈实现一个队列:[^本题考点 队列 栈]
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
……解析:
定义一个类,首先这个类要具备两个属性,一个是压栈,一个是出栈。
因为要两个栈来实现一个队列:进行插入操作的端称为队尾,进行删除操作的端称为队头。
那么如何用:两个栈实现一个队列?
栈: 先进后出
队列:先进先出
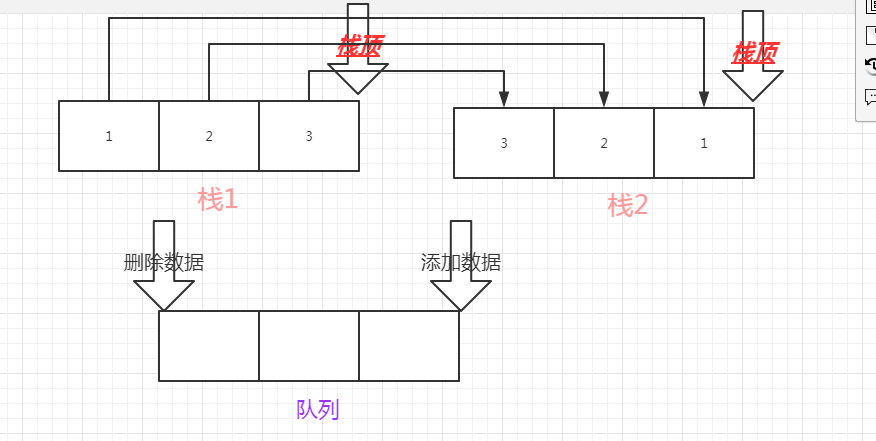
如图所示:
队列从一头添加数据,从一头删除数据。
所以我们需要让两个栈
一个栈实现添加数据
即:self.acceptStack=[]它拥有一个push的方法,用来作为队列的一端的添加数据 功能 用append来实现
self.acceptStack.append(node)
另一个栈实现删除数据:
即:self.outputStack = []它拥有pop 的方法,用来作为队列的另一端的删除数据的功能 用pop 来实现
但是我们要实现的是队列的先进先出,也就意味着 如果说我们添加数据的栈中添加了一个数据,那么我们另一个删除数据的栈中,也要相应的删除这个数据,所以说这两个栈中的数据的顺序是相反的。
以上的需求我们通过,删除acceptStack栈中的数据,在outputStack中添加这个数据,那么先在acceptStack中删除的数据,就会进入到outputStack的栈底,后在acceptStack中删除的数据,会后进入outputStack,那么它就会先出来。
那么两个栈,这样来合作,就会实现队列的先进先出,如图:1 是先进的(栈1) 那么1 就会先出来(栈2)。
进而实现了 题目的需求。
在pop 的方法中,如果说 self.outputStack是空 没有数据,那么 就给它 while 循环我们的 作为添加数据的栈
acceptStack,删除这个栈中的内容,它会弹出,然后把它添加到 栈2 outputStack 中,它就会有数据,有数据的话就返回 (如果 调用了 删除 数据的这个方法的话)。如果说 做了循环,我们的栈2 outputStack 中还没有数据,就明 acceptStack中,没有数据压入,也就说明这个 队列 没有添加数据,也就不会有删除的数据,所以返回一个None。
class Solution:
def init(self):
#添加数据栈
self.acceptStack=[]
#删除数据栈
self.outputStack = []
def push(self, node):
#向添加数据的栈中添加数据
self.acceptStack.append(node)
def pop(self):
#判断删除数据的栈中是否有数据,没有的话,就添加数据,添加数据时,要添加栈1 中删除的数据
if not self.outputStack:
while self.acceptStack:
self.outputStack.append(self.acceptStack.pop())
#如果有数据的话,就返回
if self.outputStack:
return self.outputStack.pop()
#如果没有数据,说明没有数据添加进去,也就不需要删除数据,所以返回none
else:
return None
二分查找法
分析查找:首先快速的查找方法 有二分查找法,那么什么是二分查找法?
二分查找法什么情况下用。有序的数组中。首先 肯定是在有序的 数组中的!!!!!
算法:二分法查找适用于数据量较大时,但是数据需要先排好顺序。主要思想是:(设查找的数组区间为array[low, high])
(1)确定该区间的中间位置K(2)将查找的值T与array[k]比较。若相等,查找成功返回此位置;否则确定新的查找区域,继续二分查找。区域确定如下:a.array[k]>T 由数组的有序性可知array[k,k+1,……,high]>T;故新的区间为array[low,……,K-1]b.array[k] 类似上面查找区间为array[k+1,……,high]。每一次查找与中间值比较,可以确定是否查找成功,不成功当前查找区间将缩小一半,递归查找即可。
时间复杂度为:O(log2n)。
时间复杂度
1.最坏情况查找最后一个元素(或者第一个元素)Master定理T(n)=T(n/2)+O(1)所以T(n)=O(log2n)
2.最好情况查找中间元素O(1)查找的元素即为中间元素(奇数长度数列的正中间,偶数长度数列的中间靠左的元素)
空间复杂度
- S(n)=n
二分法代码实现:
def BinarySearch(array,target):
left= 0
right= len(array)-1
while left <= right :
#除法没有移位的快
# mid = (left + right)//2
# 101 = 5 => 10 = 2
#1100 = 12 => 110 = 6
#一下用了 向右 移一位, 那么上面是解释,它就相当于 除以2 。
mid = (left + right) >> 1
#如果中间的数等于我们要找的数,那么就返回。
if array[mid] == target:
return mid
#如果说中间的数 < 目标的数,那么就说明,我们要找的数在右侧,所以左侧取值的索引需要改变为中间的索引+1;
elif array[mid]< target:
left = mid + 1
#如果说中间的数 > 目标的数,那么就说明,我们要找的数在左侧,所以左侧取值的索引需要改变为中间的索引-1; 因为越往左索引值越小
else:
right = mid-1
return None
把数组内的数据一分为二,然后计算出中间数据的 索引值。
数组中 最左侧的 索引为 0 ;最右侧的索引为 len(array)-1,数组的长度 减 1 就是 最后一个数的索引。
先判断中间索引的所对应的数组中的数值,是否与我们要查找的数字 target 相等,如果相等那么就返回,如果不相等,那么就继续判断。如果说我们找到的 array[mid] 小于 target 这个数; 那么 就说明 我们要查找的数在右侧的一半数据中,那么这个时候我们就需要改变我们左边的索引值,不在从0 开始,而是从我们中间 mid 的下一个开始,left = mid + 1,继续查找。如果说我们找到的 array[mid] 大于 target 这个数 ,那么就说明我们要查找的数据在左侧,这个时候就需要改变右侧的索引,为 right = mid-1,越往左侧走,索引值越小。直到找的的数 与target 相等为止。
以上为二分法的原理。
2. 旋转数组的最小数字 [^本题考点 查找]
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转,输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。 NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
class Solution:
def minNumberInRotateArray(self, rotateArray):
#最小值 一定比前面的要小
# 二分法查找数据 找左右的方法是:
#右边的值大于中值,就说明最小值在左边
if not rotateArray:
return 0
left = 0
right = len(rotateArray) - 1
while left <= right:
mid = (left + right) >> 1
#如果说中间的数的上一个数 > 中间数,那么就说明,我们要找的数就是这个中间的数,返回这个数。
if rotateArray[mid - 1] > rotateArray[mid]:
return rotateArray[mid]
#如果说中间的数 < 中间数的上一个数,那么就说明,我们要找的数在二分法的左侧,所以右侧取值的索引需要改变为中间的索引-1;因为越往左索引值越小
elif rotateArray[mid] < rotateArray[right]:
right = mid - 1
#否则就说明,我们要找的数在二分法的右侧,所以左侧取值的索引需要改变为中间的索引+1;因为越往右索引值越小
else:
left = mid + 1
return 0
什么叫做数组?
所谓数组,是有序的元素序列。 [1] 若将有限个类型相同的变量的集合命名,那么这个名称为数组名。组成数组的各个变量称为数组的分量,也称为数组的元素,有时也称为下标变量。用于区分数组的各个元素的数字编号称为下标。数组是在程序设计中,为了处理方便, 把具有相同类型的若干元素按无序的形式组织起来的一种形式。 [1] 这些无序排列的同类数据元素的集合称为数组。
例如:
int (32 位) int int 这三个就会组成一个数组,类型相同的变量。 a(0) a(1) a(2)
数组与python中的 列表比较相似, 用索引去查找。 数组的长度是固定的,在初始化时就指定长度。列表是可以动态增加的。 数组还和元组比较像,元组是初始化后,长度指定了就不可以变。 但是元组在初始化时给的值,确定了以后就不可以变了。 所以可以理解为数组与list 列表很相似。
3.在二维数组中的查找[^本题考点 查找]
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
class Solution:
# array 二维列表
def Find(self, target, array):
# write code here
# 1 2 3 4
# 3 4 5 6
# 4 6 8 10
# 9 11 13 15
#时间复杂度 o(n**n)
# for i in range(len(array)):
# for j in range(len(array[i])):
# if target == array[i][j]:
# return True
# return False
#时间复杂度
#O(n)
#这个二维数组的长度是多少,也就是说这个数组有几行;
row_count = len(array)
i = 0
#这个数组列数的索引值,就是我们数组取第一个数的个数,也就是有几列
column_count = len(array[0])
#给j 一个值,就是数组列数的值-1,即为j 的最大值。
j = len(array[0])-1
#循环,当i 小于我们行数的时候,并且j 也没有取到 0 那么就进入循环,去查找数据。
#我们要取到每行的最后一个数,即对应的那一列的第一个数,来与我们的目标数来对比,这个数是这一行的最大数,是这一列的最小数。
while i < row_count and j >= 0:
#根据两个索引下标可以取到 对应的在数组中的值
value = array[i][j]
#如果说取到的值,刚好等于目标值,那么就说明我们找到了它,直接返回就好。
if value == target:
return True
#如果说取到的值 > 我们的目标值。那就说明它不在它所在的那一列里,因为这个数是那一列的最小值,这个时候就需要改变我们列的索引值,给它减-1,找前一列的数做比较
elif target < value:
j -= 1
#如果说取到的值 < 我们的目标值。那就说明它不在它所在的那一行里,因为这个数是那一行的最大值,这个时候就需要改变我们行的索引值,给它加+1,找下一行的数做比较
else:
i += 1
return False
4.包含min 函数的栈[^本题考点 栈]
定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
原理:用空间换时间,用时间换空间;增加空间来减少时间的消耗
#第一种方法:考虑两个栈的长度相同,添加一个,另一个栈也会删除一个
class Solution:
#给这个类一个初始的属性,有一个栈,另外有一个最小值的列表栈
def __init__(self):
self.stack = []
self.minValue = []
#给栈中推进去数值,推进去元素node,添加函数
def push(self, node):
self.stack.append(node)
#如果最小值列表里有值
if self.minValue:
#如果最小值列表里的最后一个值 大于 node 这个值,说明node这个值小,
# 那么就放进最小值列表中;
if self.minValue[-1] > node:
self.minValue.append(node)
#如果列表里面的最后一个值,小于node值,那么就说明node这个值大;那么就添加上次添加进来的那个小的值,与栈中的数据长度保持一致;
else:
self.minValue.append(self.minValue[-1])
#如果最小值列表里面没有值,就在最小值列表里添加node
else:
self.minValue.append(node)
#给栈中做删除操作
def pop(self):
#如果说栈中是空值得话那么就返回none,说明没有在栈中压值进来,没有最小值
if self.stack == []:
return None
#栈的长度与最小值的栈的长度要相同,所以最小值列表也需要删除一个
self.minValue.pop()
#有值得话,就需要删除一个,删除做pop 操作;返回我们删除的那个数
return self.stack.pop()
#栈顶
def top(self):
#如果栈里没有数值的话,就返回一个空
if not self.stack:
return None
#否则栈里有数,那么就返回栈顶的那个数
return self.stack[-1]
#取出最小值,那么就是我们minvalue 中的最后一个值为最小值
def min(self):
#如果为空的话,就说明没有值,返回none
if self.minValue == []:
return None
return self.minValue[-1]
#第二种方法:不考虑两个栈的长度必须要保持一致,那么在栈删除值的时候,判断一下删除的值,是不是与装最小值的栈里的最后一个最小值相同,如果相同就删掉,如果不同,就不删除。
class Solution:
def __init__(self):
self.stack = []
self.minValue = []
def push(self, node):
# write code here
self.stack.append(node)
if self.minValue:
#如果最小值列表里的最后一个值 大于 node 这个值,说明node这个值小,
# 那么就放进最小值列表中;
if self.minValue[-1] > node:
self.minValue.append(node)
#最后一个值不大于node这个值得话;不做操作,不需要把它两个做的长度一致
else:
self.minValue.append(node)
def pop(self):
if self.stack == []:
return None
# write code here
#删除的时候,做个判断,它是不是与栈里面的最后一个值,与我们最小值栈里的最后一个值相等,那么就删除双方的这个值
if self.stack[-1] == self.minValue[-1]:
self.minValue.pop()
return self.stack.pop()
#如果不等的话,就只要删除栈 里最后一个值就可以
else:
return self.stack.pop()
def top(self):
if self.stack == []:
return None
return self.stack[-1]
# write code here
def min(self):
if self.minValue == []:
return None
return self.minValue[-1]
5.替换空格[^本题考点 字符串]
请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
# -*- coding:utf-8 -*-
class Solution:
# s 源字符串
def replaceSpace(self, s):
#第一种:python中自带的一个替换的函数
# return s.replace(' ','%20')
#第二种遍历来替换字符串中的空格
strlen = len(s)
#借助第三方的列表来实现时间的节省。
aaa = []
for i in range(strlen):
#如果是空格的话那就替换为%20.
if s[i] == " ":
#if s[i] isspace:
aaa.append("%")
aaa.append("2")
aaa.append("0")
else:
aaa.append(s[i])
return "".join(aaa)
6.斐波那契数列
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。n<=39
#第一种方法:下面是使用了for循环,
class Solution:
def Fibonacci(self, n):
# 如果是按照递归来写的话, 时间复杂度就是随着n的变化 增长率是 2^n
''' 递归实现
# n = 0 f(0) = 0
if n == 0:
return 0
# n = 1 f(1) = 1
if n == 1:
return 1
# if n > 1 f(n) = f(n-1) + f(n-2)
if n > 1:
num = self.Fibonacci(n-1) + self.Fibonacci(n-2)
return num
return None
'''
# n = 0 f(0) = 0
if n == 0:
return 0
# n = 1 f(1) = 1
if n == 1:
return 1
a = 1
b = 0
# if n > 1 f(n) = f(n-1) + f(n-2)
# h = a + b
# 当 n = 2 h = 0 + 1
ret = 0
#三个变量,互相转换 来实现
for i in range(0, n - 1):
ret = a + b
b = a
a = ret
return ret
#第二种方法:相对来说比较简便,简单来讲,就是取出这个列表的最后两项求和,就是列表的第三项,时间复杂度比较小,空间复杂度为 n
class Solution:
def Fibonacci(self, n):
#初始列表值 为 0 1 第三项为 0+1 = 1;
res = [0, 1, 1]
#临界条件为:第 n 项,所以就是 这个 列表的长度要小于等于 n;大于 n 就应该跳出这个循环。
while len(res) <= n:
#取出列表的最后两项,然后求和,并添加到列表中。
res.append(res[-1] + res[-2])
return res[n]
7.青蛙跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。

"""
1 (1)
2 (11,2)
3 (12,21,111)
4 (1111,22,112,121,211)
5 (11111,221,212,122,1121,2111,1112,1211)
6 (111111,222,2211,1122,2112,1221,2121,1212,21111,12111,11211,11121,11112,)
"""
class Solution:
def jumpFloor(self, number):
# write code here
#第一种方法:
res = [1, 1, 2]
while len(res) <= number:
res.append(res[-1] + res[-2])
return res[number]
a = 1
b = 1
for i in range(0,number):
a,b = b,a+b
return a
if number < 1:
return 0
if number ==1:
return 1
if number == 2:
return 2
ret = 0
a = 1
b = 2
for i in range(3,number+1):
ret = a+b
a = b
b = ret
return ret
8.变态跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
"""
1 (1)
2 (11,2)
3 (111,21,3,12)
4 (1111,22,13,31,211,112,121,4)
n 2^(n-1)
f(n) = f(n-1) + f(n-2) + .... + f(1)
f(n-1) = f(n-2) + .... + f(1)
f(n) = 2f(n-1) n > 1
f(1) = 1 n = 1
"""
# -*- coding:utf-8 -*-
class Solution:
def jumpFloorII(self, number):
# write code here
#第一种方法:
# return pow(2,number-1)
#第二种方法:
# return 2 ** (number - 1)
#第三种方法:
if number == 0:
return 0
if number ==1 :
return 1
a = 1
ret = 1
for i in range(2,number+1):
a,ret = ret,2*ret
return ret
9. 调整数组顺序使奇数位于偶数前面 [^本题知识点 数组]
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
class Solution:
def reOrderArray(self, array):
# write code here
#时间复杂度是o(n)
#空间复杂度o(n)
# ret = []
# for i in array:
# if i % 2 == 1:
# ret.append(i)
# for i in array:
# if i % 2 == 0:
# ret.append(i)
# return ret
#用了冒泡排序的原理,判断奇偶数,如果一个是偶数而且下一个是奇数,那么两个就互换位置。
for i in range(len(array)):
for j in range(len(array) - i - 1):
if array[j] % 2 == 0 and array[j + 1] % 2 == 1:
array[j], array[j + 1] = array[j + 1], array[j]
return array
知识点:冒泡排序法
def bubbleSort(array):
#一共 需要 n 次 的循环,每一个都要找到没排好序的最大值。
for i in range(len(array)):
#将没有排好序的数组 找最大值,并一直将最大值换到最顶端。
for j in range(len(array)-i-1):
#判断如果说一个数大于它下面的一个数,那么就两个数的位置互换。
if array[j] > array[j+1]:
array[j],array[j+1] = array[j+1],array[j]
return array
10.栈的压入,弹出序列 [^本题考点 栈]
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
class Solution:
def IsPopOrder(self, pushV, popV):
# write code here
#首先要先有一个栈,列表
#按照 pushV 的方式去压入栈,
# 弹出的时候是需要循环判断是否需要弹出
#判断是否需要弹出的时机,刚刚压入过后就判断
#判断需要弹出的情况的条件,压入栈的顶部和弹出栈的顶部数据相等
#先判断pushV 这个栈里是否为空,如果是空的话返回none,或者说这两个序列的长度不相同。那也返回none。
if pushV == [] or len(pushV ) != len(popV):
return None
#首先有个栈
stack = []
#定义一个变量,它作为弹出序列的索引存在。
index = 0
#遍历 pushV 的这个列表里的元素,并把它每个都添加进stack 这个列表中
for item in pushV:
stack.append(item)
#做判断 1,stack 里有元素 并且 stack里的最后一个元素 等于 popV 这个序列里 第一个元素,那么就进去这个循环,然后把stack里的这个元素删掉,这样下次还会添加新的元素,然后再和 popV 里的下一个元素 做判断,所以这个时候 index 这个索引值就要发生变化了,这个时候比较的是 它的下一个值。往右移动一位。
while stack and stack[-1] == popV[index]:
stack.pop()
index += 1
"""
if stack == []:
return True
else:
return False
"""
#最后 直到 把 pushV 里的元素都遍历完,然后stack内的元素都比较完,并都删除完,就返回True,如果说 它不为空:说明 pushV 里有的元素 是popV 中所没有的,这个时候就说明他们不相等,那么这个情况,就需要返回 False。
#以下代码与以上代码 共同实现的相同的功能,但是下面的代码相对来说等 “装B” 一点。节省代码空间。
return True if stack == [] else False
知识点链表:
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构,操作复杂。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。
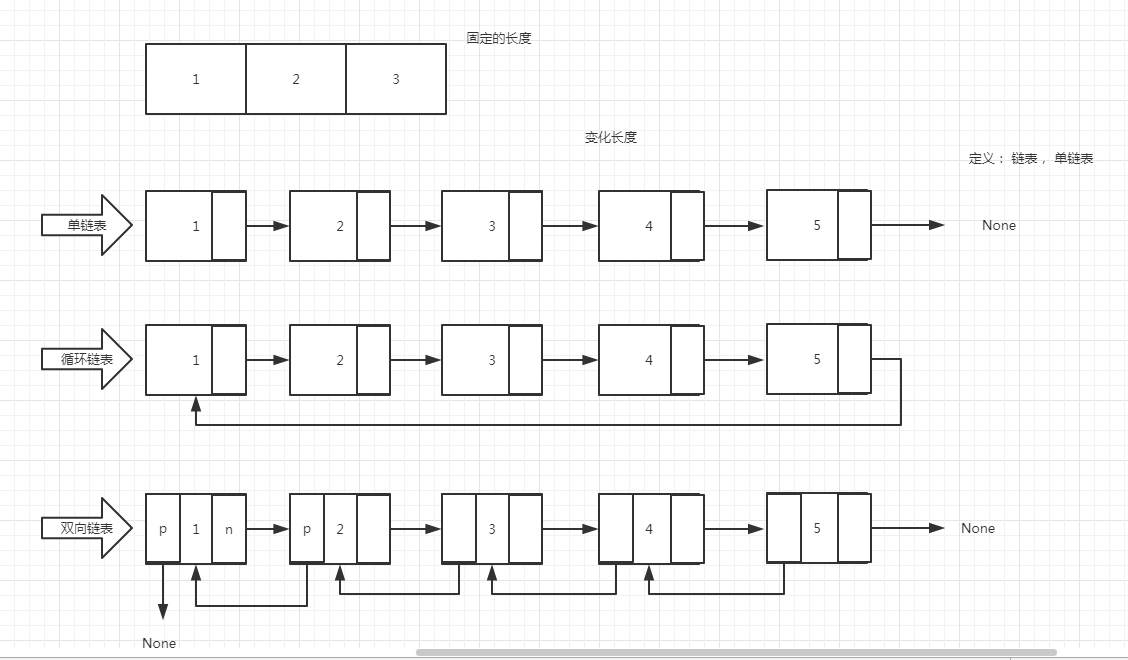
数组 就是连续的 同一个类型的 元素,而且必须是固定的长度。
如果我们想要非固定的长度来存储数据。这个时候就出现了链表。
11. 从栈尾到栈头打印链表 [^本题知识点 链表]
输入一个链表,按链表值从尾到头的顺序返回一个ArrayList。
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
# 返回从尾部到头部的列表值序列,例如[1,2,3]
def printListFromTailToHead(self, listNode):
# write code here
# pointer 指针 temporary临时数据;node 结点
#给一个 arraylist 空列表,然后向这个里面压入数据,来输出 这个链表值 的一个从尾到头 的顺序值。
ret = []
#把 listNode 这个链表 传给一个 变量
pTemp = listNode
#当这个变量 存在时 有值时:
while pTemp:
#使用 insert 的原因是:insert 可以在指定位置之前插入元素,列表.insert(索引,值)
#在空列表中起始位置,插入 pTemp的第一个值,然后 给pTemp 赋值 为 pTemp.next (下一个值)
ret.insert(0, pTemp.val)
#更改 指针,使指针指向下一个 元素
pTemp = pTemp.next
#最后返回我们 这个 插入值的 列表
return ret

如图所示:打印出 3 2 1 即为我们的目标。
12.链表中的倒数第k个结点[^本题考点 链表]
输入一个链表,输出该链表中倒数第k个结点。
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def FindKthToTail(self, head, k):
# write code here
# k 如果 比我们的链表的长度还要大的话,我们直接返回None
# k 如果小于链表的长度,我们可以定义两个变量,这两个变量中间间隔k
#用两个指针做一个尺子,然后让尺子在跳跳,然后就会找到 第k 个结点
#起始位置 第一个和第二个指针 都是从头开始的。
firstPoint = head
secondPoint = head
#首先让一个指针先开始移动,那么就是遍历我们的k 值,让我们的 第一个指针移动 k 步。
for i in range(k):
#如果第一个指针为空的话,那么说明我们的k值为空,那么我们的这个链表就为空。
if firstPoint == None:
return None
#第一个指针 移动一步
firstPoint = firstPoint.next
#当 第一个指针不为空的时候,
while firstPoint != None:
#移动尺子,移动距离为 k 的长度, 直到 第一个指针点 为空的时候 ,就到了 这个链表的结尾,此时就返回 第二个指针 那么就为 倒数第 k 个结点。
firstPoint = firstPoint.next
secondPoint = secondPoint.next
return secondPoint

如上图所示:分析过程,可以为两个结点的指针长度,也可以为三个结点的指针长度,也可以为k个结点的指针长度。
13.反转链表[^本题考点 链表]
输入一个链表,反转链表后,输出新链表的表头。
#第一种方法:
"""
pHead始终指向要反转的结点
last 指向反转后的首结点
每反转一个结点,
把pHead结点的下一个结点指向last,
last指向pHead成为反转后首结点,
再把pHead向前移动一个结点直至None结束
"""
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
# 返回ListNode
def ReverseList(self, pHead):
#首先判断这个链表里是否只有一个结点,只有一个结点那么它就不需要发生变化,它第一个结点指向的指针就为 none
# 这个时候就直接返回这个 pHead
if not pHead or not pHead.next:
return pHead
#首先要明白 反转过后,第一个数值的指针的结点指向的是none 也就是一个指向反转后的首结点 为none
last = None
#当 要反转的结点 pHead 存在的时候
while pHead:
#先找到第一个元素的结点指向的元素,赋值给一个临时变量
temp = pHead.next
"""
本来一个元素的结点 是要指向它的下一个 元素的 .
反转后 就是 这个元素 要指向它的 上一个 元素 .
"""
#然后第一次循环 把这第一个元素的结点 改为 none last 第一个值 是 none (此时还没有发生改变的last)
# 之后循环 就是 每 反转一个结点 把pHead结点的下一个结点指向last,
pHead.next = last
#下一步 是把 pHead 这个 元素的 赋值给last
# last指向pHead成为反转后首结点,
last = pHead
# 再把pHead向前移动一个结点直至None结束
pHead = temp
return last
"""
反转需要两步 ,第一步找到它的 结点,第二步改变结点就可以了;
之后需要 把结点 赋值为 这个元素的 本身 ;
循环:
找到 元素结点指向的元素,
目标是 让元素结点指向的元素 改为 自己本身。
"""
#第二种方法:
"""
1 将现有的头换成尾,尾部的next为空
2 将从第二个node开始,循环将next指向前一个
3 需要一直有一个指针指向还没有反转的链表的头部
"""
class Solution2:
# 返回ListNode
def ReverseList(self, pHead):
#判断是否为空值,没有元素
if pHead == None:
return None
#判断是否只有一个元素
if pHead.next == None:
return pHead
#左边指针为 头 第一个 指针
leftPointer = pHead
#中间 的指针 为 第二个指针
midPointer = pHead.next
#右边的指针 为 指向 中间 指针后的 所有的元素
rightPointer = midPointer.next
#左边的指针为 起始 的 元素, 反转后 它的next 为 None;
leftPointer.next = None
#循环,当我的右边的结点指向的 元素 一直存在的时候,那么就会一直循环,一直来反转结点。
while rightPointer:
#中间指针指向的为上一个 元素 即 leftPointer
midPointer.next = leftPointer
#三个指针开始往右移。每次移一个。
#左边指针 往右移一个 就是中间指针的位置
leftPointer = midPointer
#中间指针 往 右 移 一个,就时 右边指针的位置
midPointer = rightPointer
#右边指针往右移 一个 ,就时 右边指针的下一个。
rightPointer = rightPointer.next
#当右指针 指向的为 空的时候 就会跳出循环,那么此时的最后一次循环的 中间的指针的 指向的 是此时的左 指针。
midPointer.next = leftPointer
#最后返回中间的 这个指针,就是 最后一个 反转的指针的第一个,表头。
return midPointer
如图所示:

14.复杂链表的复制
输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针指向任意一个节点),返回结果为复制后复杂链表的head。(注意,输出结果中请不要返回参数中的节点引用,否则判题程序会直接返回空)
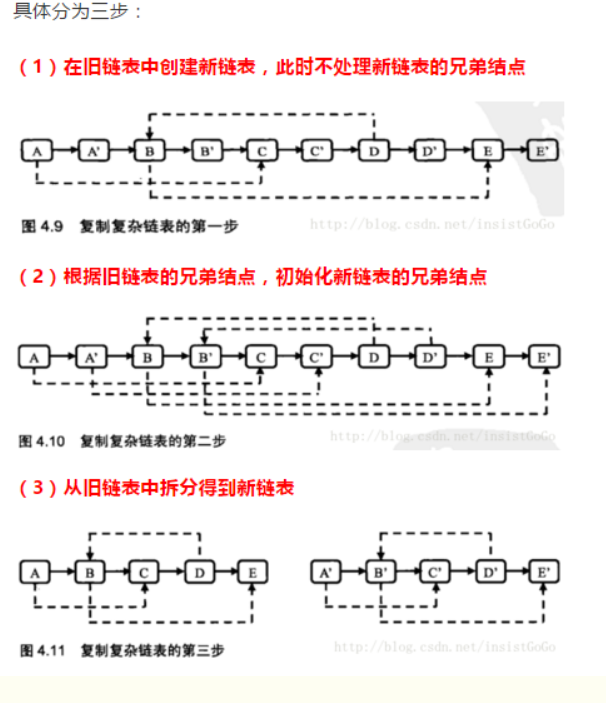
#第一种方法:
# -*- coding:utf-8 -*-
# class RandomListNode:
# def __init__(self, x):
# self.label = x
# self.next = None
# self.random = None
class Solution:
# 返回 RandomListNode
def Clone(self, pHead):
# write code here
#判断当pHead 为空值的时候 返回的是none
if pHead == None:
return None
# 复制一个一样的node, 并且添加到之前的链表的每一个node后面
pTmp = pHead
while pTmp:
#把第一个 A 的值 赋给 node 为A‘
node = RandomListNode(pTmp.label)
#此时 node A' 的结点指向的是 原来A 的结点指向的 值
node.next = pTmp.next
#将原来A 的结点指向的值 改为 A’
pTmp.next = node
#将 我们要操作的指针 向后移动 操作下一个 需要复制的元素,即为 A‘ 结点 指向的元素
pTmp = node.next
# 实现新建的node的random的指向
pTmp = pHead
while pTmp:
#如果现在操作的这个指针的元素,存在一个 random 的结点
if pTmp.random:
#那么 这个A 的结点指向的(A’)的random结点指向的 值 为 A 的random的结点指向的值,指向的结点(也就是它的下一个值)上图更清楚明白。
pTmp.next.random = pTmp.random.next
#建好 这个元素的 random 的值,然后移动 指针 到下一个元素,来 建立 下一个 复制的元素的random 结点的指向。
#当前元素 下一个的下一个 是复制的元素 是需要添加random 指向的元素。
pTmp = pTmp.next.next
# 断开原来的node 和 新的node 之间的链接
#最后 为断开 链接 的操作
pTmp = pHead
#复制的新链表的表头A’ 为 旧链表 A 的结点指向的 下一个值A‘
newHead = pHead.next
#复制的新链表的第一个值A’ 为 旧链表 A 的结点指向的 下一个值A‘
pNewTmp = pHead.next
while pTmp:
#print(pTmp.label)
#将旧链表 A 的指向结点 改为 A‘ 的指向的下一个 的B。
pTmp.next = pTmp.next.next
#如果新的 链表 的元素有指向的下一个的指针
if pNewTmp.next:
#那么就把 这个元素的A’ 的结点指向 改为 A‘ 下一个 B 的下一个 的B’
pNewTmp.next = pNewTmp.next.next
#然后再 将 新链表的指针移 位,来断开下一个 链接,也就是 指针改为了 B‘
pNewTmp = pNewTmp.next
#上面新链表的元素指针改好了,再更改 下一个旧链表的 元素 也就是 上三行代码 之前改好的 A 的结点指向的B
pTmp = pTmp.next
#如此循环下去,改变所有的 新链表,旧链表的指向。
#最后返回这个复制好的新链表。
return newHead
#第二种方法:
import copy
chead=copy.deepcopy(pHead)
return chead
15.两个链表之间的第一个公共结点
输入两个链表,找出它们的第一个公共结点
如图:

# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def FindFirstCommonNode(self, pHead1, pHead2):
# write code here
pTmp1 = pHead1
pTmp2 = pHead2
#当链表1 和链表2 同时存在的时候
while pTmp1 and pTmp2:
#当两个链表移动到值相同的时候,这个位置就是结点,直接返回pTmp1或pTmp2
if pTmp1 == pTmp2:
return pTmp1
#移动指针的位置,两个同时移动,
pTmp1 = pTmp1.next
pTmp2 = pTmp2.next
#第一个参数给比较短的那个链表的值
#第二个参数给比较长的链表的值
#第三个参数是比较短的那个链表头
#第四个参数是比较长的那个链表头
def findEqual(longPointer, shorPointer, longHead, shortHead):
k = 0
# 寻找出链表长度之间的差值,让长的链表继续走,直到链表走完为止,走了多少步,就说明,两个链表之间的差值是多少。
while longPointer:
longPointer = longPointer.next
k += 1
#然后:
# 先让长的那个去走k步
longPointer = longHead
shortPointer = shortHead
for i in range(k):
longPointer = longPointer.next
#长的走k步之后,再让两个链表一起移动,直到两个链表移动的位置的值相等为止,那么这个点就是 两个链表的第一个公共结点。
while longPointer != shortPointer:
longPointer = longPointer.next
shortPointer = shortPointer.next
return shortPointer
#如果两个链表不一样的长度,那么假设是 第一个链表长度长,第二个链表已经走完了,结束了,那么第一个链表还没有走完,那么就调用我们封装好的函数,或者是看下面注释的代码。
if pTmp1:
return findEqual(pTmp1,pTmp2,pHead1,pHead2)
# k = 0
# #寻找出链表长度之间的差值
# while pTmp1:
# pTmp1 = pTmp1.next
# k += 1
# #先让长的那个去走k步
# pTmp2 = pHead2
# pTmp1 = pHead1
# for i in range(k):
# pTmp1=pTmp1.next
#长的走k步之后,再让两个链表一起移动,直到两个链表移动的位置的值相等为止,那么这个点就是 两个链表的第一个公共结点。
# while pTmp1 != pTmp2:
# pTmp1 = pTmp1.next
# pTmp2 = pTmp2.next
# return pTmp1
if pTmp2:
return findEqual(pTmp1, pTmp2, pHead1, pHead2)
# k = 0
# # 寻找出链表长度之间的差值
# while pTmp2:
# pTmp2 = pTmp2.next
# k += 1
# # 先让长的那个去走k步
# pTmp2 = pHead2
# pTmp1 = pHead1
# for i in range(k):
# pTmp2 = pTmp2.next
#长的走k步之后,再让两个链表一起移动,直到两个链表移动的位置的值相等为止,那么这个点就是 两个链表的第一个公共结点。
# while pTmp1 != pTmp2:
# pTmp1 = pTmp1.next
# pTmp2 = pTmp2.next
# return pTmp2
16.合并两个排序的链表 [^本题考点 链表]
输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。
如图:为两个递增的链表

如下图,合并成一个单调不减链表

#第一种方法:
"""
比较两个链表的首结点,哪个小的的结点则合并到第三个链表尾结点,并向前移动一个结点。
步骤一结果会有一个链表先遍历结束,或者没有
第三个链表尾结点指向剩余未遍历结束的链表
返回第三个链表首结点
"""
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
# 返回合并后列表
def Merge(self, pHead1, pHead2):
# write code here
head = ListNode(0)
tmp = head
while pHead1 is not None and pHead2 is not None:
if pHead1.val <= pHead2.val:
tmp.next = pHead1
pHead1 = pHead1.next
else:
tmp.next = pHead2
pHead2 = pHead2.next
tmp = tmp.next
if pHead1 is None:
tmp.next = pHead2
elif pHead2 is None:
tmp.next = pHead1
return head.next
#第二种方法:
class Solution:
# 返回合并后列表
def Merge(self, pHead1, pHead2):
# write code here
#首先判断两个链表是不是为空。
if pHead1 == None:
return pHead2
if pHead2 == None:
return pHead1
#比较两个链表当前指针的元素值的大小。小的那一方为新的一个表头。
newHead = pHead1 if pHead1.val < pHead2.val else pHead2
pTmp1 = pHead1
pTmp2 = pHead2
#判断 如果新表头 是 表1 的头的话 那么 新表头
if newHead == pTmp1:
pTmp1 = pTmp1.next
else:
pTmp2 = pTmp2.next
#
previousPointer = newHead
while pTmp1 and pTmp2:
if pTmp1.val < pTmp2.val:
previousPointer.next = pTmp1
previousPointer = pTmp1
pTmp1 = pTmp1.next
else:
previousPointer.next = pTmp2
previousPointer = pTmp2
pTmp2 = pTmp2.next
if pTmp1 == None:
previousPointer.next = pTmp2
else:
previousPointer.next = pTmp1
return newHead
17.圆圈中最后剩下的数 [^本题考点 模拟]
每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0…m-1报数….这样下去….直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!^_^)。请你试着想下,哪个小朋友会得到这份礼品呢?(注:小朋友的编号是从0到n-1)

思路分析:
这个题一开始小朋友们每个人自己的编号是确定的,就相当于我们列表里面的索引是确定的一样,然后让编号为0。
链表1:也就是 列表里面的第一个数开始报数,上图第一个链表蓝色的0,开始报数。报到 m-1 的数的 i小朋友 出列,圈里就少了一个数。定义为 f(n).
链表2:这个时候 从 m-1 的下一个 m 开始 下一轮的循环,开始报数,也就是上图第二个链表的蓝色框。再次报到 m-1 的时候,这个ii小朋友会站出来。(但是这个时候 我们链表的 循环顺序 (m-(m-2)) 发生了变化,不再是从第一个数 【链表的表头 开始循环,而是m 这个数作为起始位置的】,与之前第一个 链表循环的时候的 顺序(0-n)不同了【起始位置为链表的表头】。此时表里少了一个小朋友。这个是题意,让我们这样来找的小朋友。所以定义为 f `(n-1).
这样的话,就出现了 上图中的 链表2 ,链表3. 这样的不同的情况,这两个 找出来的第 m-1 个 小朋友 是同一个小朋友,但是 两个顺序却不相同。
链表3:这个图 是 以 m 为起始位置 来寻找第 m-1 个值的,它 就是 f(n-1)
如果说我们想由 链表3 得到 链表2 的话,那么 我们就需要把作为起始位置的m(下标为0) 移动到 下标为(m) 的位置,那么就是下标值 + m 。如图,我们需要移动的是 每个数值所对应的 下标 index值。让 m 在一个链表中作为起始位置来开始 报数 找 第 m - 1 个iii小朋友。
但是又由于 我们这样直接加上一个m 以后,这个 index 值有可能会大于 这个链表的长度,如果大于这个链表的长度的话,那么就是说移动到了这个链表的前一部分,所以要对我们的 这个数 对 链表的长的的一个取余:
(iii+m)%n 我们一共是 n 个值,从0-(n-1);
f(n-1) = iii
所以 f(n) = f `(n-1) = (iii+m)%n
所以 f(n) = (f(n-1)+m)
那么这个通项表达式我们就找到了,再去编写代码。
# -*- coding:utf-8 -*-
class Solution:
def LastRemaining_Solution(self, n, m):
# write code here
#通过推导公式可得 f(n) = (f(n-1)+m)%n
#首先判断,当我们这个链表里没有小朋友的时候,或者找到的小朋友报的数小于1 的时候,这个时候返回一个-1,题中表示 如果测试的是0个小朋友,数0个站出来,那么返回的值应为-1.
if n < 1 or m < 1:
return -1
#只有一个人的时候,说明要找的就是这一个人。那么就返回下标0 编号。
if n==1:
return 0
value = 0
#时间复杂度 o(n)
#从 2 开始 一直到 n 个小朋友 来循环,n 个数,所以为 n+1
for index in range(2,n+1):
#现在数到的 m-1 这个值 的索引。对应上上面的公式。
currentValue = (value+m) % index
#把找到的这个下标值 赋值给 value
value = currentValue
#返回编号
return value
18.链表中环的入口点 [^本题知识点 链表]
给一个链表,若其中包含环,请找出该链表的环的入口结点,否则,输出null。
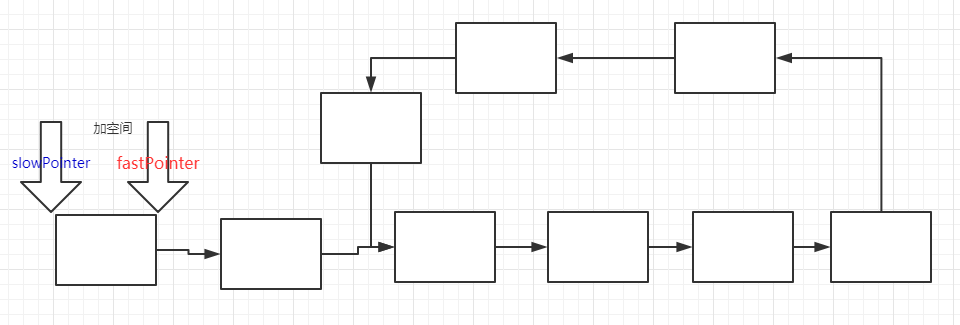
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def EntryNodeOfLoop(self, pHead):
# write code here
#首先需要定义两个指针,其中一个快,跳两步,一个慢跳一步。
#循环跳
#要么是快的指针 为 none(没有环),要么是快慢指针相等(有环)。
if pHead == None:
return None
#定义两个指针,一个快的一个慢的。
fastPointer = pHead
slowPointer = pHead
#当快指针存在时,而且快指针的结点指向的下一个也存在
while fastPointer and fastPointer.next :
#那么让快指针走两步
fastPointer = fastPointer.next.next
#让慢指针走一步
slowPointer = slowPointer.next
#如果慢指针等于快指针时,那么就说明这个链表中有环。有环的话那么就跳出,break
if fastPointer == slowPointer:
break
#如果说两个指针没有相等的时候,快指针就已经走到链表的尽头了,说明这个链表没有环。那么就返回None。
if fastPointer == None or fastPointer.next == None:
return None
#如果slow 走了 l 的长度 那么 fast 就走了 2l 的长度
#假设 从开始到入口点的长度是 s;slow 在环里面走的长度是 d
# 那么 L = s + d
#假设 环内 slow 没走的 长度 是 m; fast 走的长度是多少
# fast 走的长度 就是 ( m + d ) * n + d + s = 2 L
#带入 ( m + d ) * n + d + s = 2 (s + d )
# s = m + (n-1)(m+d)
#有环的话,那么就让快指针从头开始走,这次一次走一步,
fastPointer = pHead
#此时慢指针还在环里走着,没有走到结点
while fastPointer != slowPointer:
fastPointer = fastPointer.next
slowPointer = slowPointer.next
#当两个指针相等时,就会相遇,这时返回一个指针的值,就为 入口结点处。
return fastPointer
定义:
假设 slow 走了 L 步,那么 fast 就走了 2L 步。
我们 链表的头部 到 链表的环的入口结点处 的距离是 S
那么 从入口结点 到 我们 快慢指针相遇的地点 的距离 为 d。
链表的环中,慢指针走过的距离是d,那么没走过的距离是M。
我们不确定的是快指针在链表的环里走过了多少圈来与慢指针相遇,因此 将这个参数设置为n。
那么 L = s + d
2L = 2(s+d) = n*(m + d) + d + s
由上面公式 推导出 n(m+d) = s + d
得到:s = n(m+d) -d;
s = nm + (n-1)(d) s = m + (n-1)(m+d)
19.二进制中的1的个数
输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示
知识点:
补码
特性:
1、一个负整数(或原码)与其补数(或补码)相加,和为模。
2、对一个整数的补码再求补码,等于该整数自身。
3、补码的正零与负零表示方法相同
按位取反 ~
~,用法只有一个那就是按位取反,需要注意的是:
- ~的按位取反,包括符号位
- 正数各位取反变为负数,显示时转化为其补码
- 负数本身需要先转换为补码(符号位不变,各位取反再加 1),再对其补码进行各位去反
1. ~5
5 的二进制为 0101,
~5
- (1)各位取反,1010
- (2)变为负数,转化为其补码形式(符号位保持不变),各位取反 1(1101),再加1(1110),也即 -6
>> ~5
>> -6
2. ~(-5)
-5 因为是负数,存储时存储的是其补码:
- -5 的补码是:1011,
- ~(-5)将其各位取反(包括符号位),也即 0100(4)
>> ~(-5)
>> 4
# -*- coding:utf-8 -*-
#第一种:
class Solution:
def NumberOf1(self, n):
# write code here
#补码:正数不变,负数是它的正数的反码 + 1
# -2 补码: -2 的 1 0000.。。000010,
# 1 1111.。。111101 + 1
#-2 的补码就是 1 1111.。。111110
#把输入的正数n转化为二进制的数,并把0b 替换掉,计算1的数量,如果输入的值不是正数的话
#一个负整数(或原码)与其补数(或补码)相加,和为模。2 的32 次方 是模。
#那么就是 2 的32 次方 然后 + n 这是在取一个负数的补码 就相当于 n & 0xffffffff
#然后计算 这个数里面 1 的 数量
return bin(n).replace("0b", "").count("1") if n >= 0 else bin(2 ** 32 + n).replace("0b", "").count("1")
#第二种:
# -*- coding:utf-8 -*-
class Solution2:
def NumberOf1(self, n):
# write code here
# 1 出现的次数为0 次
count = 0
#判断 这个数 n 是不是负数,如果是负数的话 求其补码:
if n < 0:
n = n & 0xffffffff
#如果这个数不是0 的话,那么它在二进制的表示中至少有一位是1,所以一开始我们赋值 count +=1.
while n:
count += 1
#把一个整数先减去1,再和原整数做与运算,会把该整数最右边的1 变从成0,那么一个二进制中有多少个1,就可以进行多少次这样的操作。
n = (n - 1) & n
return count
"""
例如:一个二进制1100, 它的第二位 是从最右边数起的一个1,减去一个1后,第二位变成0,它后面的两位0变成1,而前面的1保持不变,因此结果是1011.
那把 这个整数 和它 减去1 的结果 做一个按位 与运算,相当于 把 最右边的 1 变成 0,。
1011 和 1100 做 按位与 运算 1100 & 1011 结果为 1000,那么刚好是我们 要得到 将最右边的1 变成0 的结果 1000.
"""
20.不用加减乘除做加法[^本题考点 按位运算]
写一个函数,求两个整数之和,要求在函数体内不得使用+、-、*、/四则运算符号。
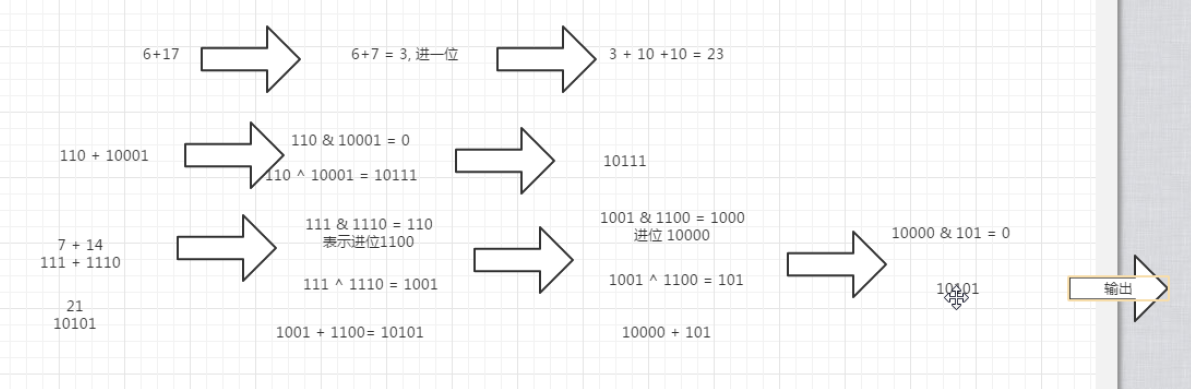
分析:
对于数字运算,如果说四则运算不能用的话,那么我们只能用位运算来做了。
我们以 5 + 17 为例 结果为 22,那么 22 的计算结果,我们可以分为三步 来进行:
第一步: 只做各位相加不进位 也就是说 没一位上的数字 相应的来相加 但是不进位,那么 5 + 7 为 12
个位数 5 和 7 相加 不进位 是2 十位是0 和1 相加 为 1
第二步: 5 + 7 中有进位,进位值 是10 ;
第三步: 把前面两个结果 加起来: 12 + 10 = 22
以上为我们用十进制计算的 策略,那么 我们用于位运算中是不是也合适,我们来举个栗子:
还是以 5 + 17 为例,那么 5 的二进制是101 ; 17 的二进制是 10001;
第一步:各位相加 但不进位: 101 + 10001 = 10110 不进位的话 结果为 10100 (最后一位两个数都是1,相加的结果需要进位,但是这一位不进位,意味着结果仍然是0)
第二步: 记下进位,它只在最后一位相加时产生了一个进位。
第三步: 把前面两个结果相加,得到的结果是 10110.
那么现在我们把前面的 二进制的加法用位运算来替代的话
第一步的 求 和 运算就是 不考虑 进位的话,对每一位来相加,0 和0 1 和1 的结果都是0,0+1,或者1+0 的结果 都是1;那么我们会看出它与我们学过的异或运算相同,就是相同为假,不同为真,所以叫 异 或 XOR 。
第二步: 对0 加 0、1加0、0加1 而言,都不会产生进位,只有1+1 的时候,会产生一个进位。此时 我们可以想象成两个数 先做了一个 位 与 & 运算,然后再向 左移 一位。只有两个数是1 的时候,位与 & 得到的结果是 1,其余的都是0。
第三步:把前面两个步骤的结果再相加,然后在继续判断是否有进位,直到没有进位为止,那么此时的相加的过程,依然是重复前面的两步,直到不产生进位为止。
# -*- coding:utf-8 -*-
class Solution:
def Add(self, num1, num2):
#第一种代码:循环。简洁但是原理相同,那么我们以下面第二段代码为例;来解析。
# while (num2):
# num1, num2 = (num1 ^ num2) & 0xFFFFFFFF, ((num1 & num2) << 1) & 0xFFFFFFFF
# return num1 if num1 <= 0x7FFFFFFF else ~(num1 ^ 0xFFFFFFFF)
#第二种代码:
#首先两个数做 一个 异或 运算^ 那就是 在不进位的情况下,让两个相加 求和。
xorNum = num1 ^ num2
#让两个数 做 位与 操作,然后再向 左 移 一位,得到它 向前进位的值。
andNum = (num1 & num2) << 1
#判断,当 进位 的值不等于0 的时候,说明 一直有进位,也就是 过程没有结束。
while andNum != 0:
#那么我们就继续上面的操作。但是这次的 数值 改为上次的两个结果,
#一个 是异或的结果,一个是 与 操作 & 以后 左移一位的 结果。
tmp1 = xorNum ^ andNum
tmp2 = (xorNum & andNum) << 1
#因为如果这个数为负数的话,那么负数 左移 一位与正数 不同,负数 是数值变小,正数 数值变大
#如果是正数的话那么这一步就 不变,如果是负数的话,这一步就对负数来起作用。
#对于python来说 负数的 二进制 可能会有无数个1,我们用这个方法让它变成一个可数的数字长度。
tmp1 = tmp1 & 0xffffffff
xorNum = tmp1
andNum = tmp2
#一个负整数(或原码)与其补数(或补码)相加,和为模。 0xffffffff
# ~(xorNum ^ 0xFFFFFFFF) 这个是 异或数 与 模 来 异或,最后 按位 取反 来求得 负数的补码。
return xorNum if xorNum <= 0x7ffffff else ~(xorNum ^ 0xFFFFFFFF)
21.数组中出现次数超过一半的数字[^本题考点 数组]
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
思路:抵消掉 遇到不相同的数字就相互抵消掉,最终剩下的数字就可能是出现次数大于数组长度一半的数字。 首先我们来遍历数字,遍历的时候需要记录上次出现的数字是什么,进而判断 下次出现的数字是否与现在这个数字相等,如果不相等的话,那么就把两个数字抵消掉,到最后没有抵消掉的数字,就可能是出现的次数大于数组长度的一半。
我们可以考虑在遍历数组的时候保存两个值:一个是数组中的一个数字,另一个是次数;当我们遍历到下一个数字的时候,如果下一个数字和我们之前保存的数字相同,则次数加1,如果下一个数字和我们之前保存的数字不同,则凑数减1.如果次数为0 ,我们需要保存下一次出现的次数,然后把次数设置为1.
# -*- coding:utf-8 -*-
class Solution:
def MoreThanHalfNum_Solution(self, numbers):
# write code here
#dict [key] = count
#o(n) 空间复杂度为O(n)
#第一种思路:建 一个字典,把数字作为键,数字出现的次数作为值,然后 遍历这个数组中的数,如果这个数作为键出现过,那么就让他的值加1,如果没有就把它添加到字典中。
numsCount = {}
numLen = len(numbers)
for num in numbers:
if num in numsCount:
numsCount[num] += 1
else:
numsCount[num] = 1
#如果说字典中某个键 大于 我们这个数组长度的一半,那么就返回这个键, 数组长度的一半 可以用 >> 1右移以为来实现,右移以为相当于 是除以2.
if numsCount[num] > (numLen >> 1):
return num
return 0
#想要空间复杂度为O(1),时间复杂度为o(n)
#第二种:
#定义变量 上次出现的数字为0
last = 0
#上次出现的数字的数量为0
lastCount = 0
#遍历数组中的数字
for num in numbers:
#如果说这个数字出现的次数为0了。
if lastCount == 0:
#那么就把上次出现的数字,变为需要保存的那个数字。
last = num
#并把次数设置为1 次,出现了这一次。
lastCount = 1
else:
#否则就判断,这个数字是不是与上次出现的次数相同,如果相同的话,那么我们这个数字出现的次数就加1.
if num == last:
lastCount += 1
#如果不同的话,那么我们就让这两个数字抵消掉,那么这个数字出现的次数需要减 1;
else:
lastCount -= 1
#如果最后遍历完事之后 这个记录数字出现次数的 值为0 的话,那么就说明我们的这个数组里面的数刚好可以两两抵消掉
if lastCount == 0:
return 0
#否则的话,就说明 数组里面 留下了没有抵消掉的数
else:
#这种情况是last可能是大于一半的数字
#这个时候把 记录数字次数的变量 计数 为0
lastCount = 0
#遍历数组中的数
for num in numbers:
#如果这个数与我们记录的数相等的话
if num == last:
#让这个计数加1
lastCount += 1
#最后判断一下,这个数的计数次数,是不是大于 我们数组长度的一半,如果是的话,就返回这个数,如果不是就返回0.
if lastCount > (len(numbers)>> 1):
return last
return 0
22.数组中只出现一次的数字[^数组]
一个整型数组里除了两个数字之外,其他的数字都出现了偶数次。请写程序找出这两个只出现一次的数字。
思路:其他数字出现的次数都是偶数次,那么我们就可以用到异或的一个性质,那就是 任何一个数字异或它自己都等于0.,也就是说如果我们 从头到尾 异或 数组中的每个数字,那么最终的结果刚好是那个 只出现一次的数字,因为那些成对出现的数字都已经全部抵消掉了。
# -*- coding:utf-8 -*-
class Solution:
# 返回[a,b] 其中ab是出现一次的两个数字
def FindNumsAppearOnce(self, array):
# write code here
#如果两个数相同那么两个数的异或操作为0
#数组的长度如果小于2,那么就就不会有数字出现了偶数次。
if len(array) < 2:
return None
#变量赋值 两个数的异或为none
twoNumXor = None
#遍历 数组中的数字
for num in array:
#判断 如果 两个数的数字异或的结果为0 的话,
if twoNumXor == None:
#那么 此时就让 两个数异或中的一个数 为此时遍历出来的那个数。
twoNumXor = num
#如果数 这个数不为 空 的话
else:
#那么就让这个 两个数异或的结果的值 (或者当 异或的值为空的时候,我们赋给的值 与 此时遍历数组中的数得到的 num 来异或。
twoNumXor = twoNumXor ^ num
#变量 计数 为 0
count = 0
#当异或的 结果 为偶数时
while twoNumXor % 2 == 0 :
#那么我们就给它 除以2 ,每除一次2 就记录一次,直到 结果不为 奇数 为止。
twoNumXor = twoNumXor >> 1 # 右移以为 相当于 除以2
count += 1
#以上是用来计数 判断 这个 二进制数中 第一个1 是在哪一位上。
#我们在这个结果中 找到 第一个为1 的位的位置,记为 第 n 位,那么 现在我们以第n 位 是不是 1
mask = 1 << count #向左 移 位 count 位。
#为标准 把原 数组中的数字分成两个子数组,第一个数组中每个数字的第n 位 都是1,而 第 二个子 数组中的 每个数字的第 n 位 都是 0.由于我们的分配的标准是 数字中的某一位是0 还是1 ,那么数字相同的数肯定被分到了 同一组,那么每个 子数组中 都会包含一个 只 出现一次的数字,而 其他数字都出现了两次,这个时候,分别把 子数组中的 所有的数 异或,那么 最后的结果 就是 那个 出现一次的数。
firstNum = None
secondNum = None
for num in array:
if mask & num == 0:
if firstNum == None:
firstNum = num
else:
firstNum = firstNum ^ num
else:
if secondNum == None:
secondNum = num
else:
secondNum = secondNum ^ num
return firstNum,secondNum
23.整数中1出现的次数[^本题考点 数组]
求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数?为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数(从1 到 n 中1出现的次数)。

如上图所示,如果那个数 是我们 的 1-n 中 n 这个数,那么这个数就是一个特别大的数,不能遍历 计算每个数字的1 的个数, 那就只能去寻找1在数字中出现的规律来。
那么我们可以把 这个数字中 ,分段来 看 1 在这个数字片段中可能出现的情况都有多少。
**若 以上 栗子 中的 十万位上的 0 那一位 为 数字1 的话,有多少种 可能? **
首先 直接 为1 的话,这个数就会大于 我们的n 这个数,所以 它需要 向前一位借 一位,来计算 可能出现的 情况 有多少种,那么就是 一共 有
0-3458 个数 那么就一共是 3459 中可能性。
那么十万位 后面 出现1 的情况有多少种 可能性 ?
0 后面一共有5 位,每 一 位 的数字 可能的情况 是 0-9 共 十 个数字,也就是说 后面 为的可能性是 10^5.
那么就是说对于 十万位数字是0 来说,一共有3459*(10^5 )种 可能。
接下来我们在考虑一个 数字 那就是 万 位 上的数字,8,如果8 这一位为1 的话,有多少种可能性?
如果8 为1 的话,那么就是我们前面的数字 有 1-34590,共34591种情况,后面 是一共 4 位,那么就有 10^4种情况。
那么就是说对于 万位数字是0 来说,一共有34591*(10^4) 种 可能。
我们再考虑另一个特殊的,那就是我们的百位上的 1 那一位,除了现在的n 的百位上是1,那么其他 这个一位为1 的情况,一共有多少种可能?
如果说1 这个数字不变的话,那么1前面 的位数 可能为1 的可能性就是 0-3459082,后面的两位的 可能性为 0-90,不能大于90,如果大于的话,需要 跟 百位来借 一位了,我们先考虑这种不借位的可能性,那就是
3459083*91,如果借位的话,那么前面就是 0-3459081,后面就10^2-91 为9 种 情况,那么最后 一共有
3459083 x 91+3459082 x 9,最后推导为 3459082 x 91 + 91 + 3459082 x 9,最后为 3459082 *10^2 +91种 可能性。
分析了三种特殊的情况,那么我们可以用递归的方式来找,只不过因为递归的话 时间复杂度比较高,那么我们可以写一个 与递归等价的 while 循环来实现,递归和 while 循环是可以互相转换的。
class Solution:
def NumberOf1Between1AndN_Solution(self, n):
# write code here
#循环的出口是 highValue = 0
#我们从最低位开始一个位一个位的来寻找 1 的可能出现的 情况次数。
# 一开始 精准度为1.高位低位中位 先赋值为1.
preceise = 1
highValue = 1
lowValue = 1
midValue =1
#计数 后面的位数。
count = 0
#计数 1 的次数和
sumNum = 0
#循环的 出口是我们找不到最高位了,那么这个时候就说明,我们遍历到了 这个数字的最高位。
while highValue != 0:
#高位 先将这个数 除以10 得到高位
highValue = n // (preceise * 10)
#中位 先将这个数 与 10 取余。
midValue = (n // preceise)%10
#低位 先将这个数 除以 1 那么低位就是个位后面的,没有就是0.
lowValue = n % preceise
#每遍历一次 向右移一位,那么就是说 精准度要乘以10.
preceise *= 10
#如果这个数是0 的话,
if midValue == 0:
#那么它就是高位的值,乘以 10^后面的位数 次方,但是这个时候 对于中位 来说 它是个位,后面没有位,所以是0,
num = (highValue)* pow(10,count)
#如果这个数 大于1 的话,
elif midValue > 1:
#那么它 就是 最高位加1 乘以 10^后面的位数 次方,
num = (highValue+1)*pow(10,count)
else:
#否则的话 它就是等于1 的情况了,对于等于1 的1情况,又是比较特殊的情况,它需要 最高位 * 它10 的后面位数个数的次方,然后要加上我们低位 的数值再加 1, 原因在上面的分析中已经给出。
num = highValue*pow(10,count)+(lowValue+1)
#最后 我们1 出现的 次数 就是这 三个 num 的和,。
sumNum += num
#没循环一次,这个三个就往左移一次吗,那么这个时候它们 后面的位数也就会 多一位。
count += 1
#最后返回这个 次数和。
return sumNum
24.丑数
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
思路分析 第一种方法:所谓的一个数n 的因子,是指 n 能被m 整除,也就是 n%m == 0; 根据丑数 的定义,丑数只能被 2,3,5 整除,也就是说,如果一个数能被2 整除,能被3 整除,能被5 整除,如果最后的到的数是1.那么这个数就是丑数,否则就不是。 先搞清楚丑数的定义是什么?
因此按照这个思路我们就可以 写出下面的 代码。但是 这个代码 是逐个判断的每个整数是不是丑数的解法,它直观,但是不够高效,最大的问题是 一个不是丑数的数,我必须要计算 而且判断它是不是丑数。
class Solution:
def GetUglyNumber_Solution(self, index):
# write code here
if index < 1:
return None
#死循环,找丑数
#判断一个数是不是丑数,先循环除以2,直到不能整除,
#循环除以3 直到不能整除,循环除以5 直到不能整除
#这时如果剩余的值是1 我们就说它是丑数
#其他情况就都不是丑数
def isUglyNumber(num):
while num % 2 == 0:
num = num //2
while num % 3 == 0:
num = num //3
while num % 5 == 0:
num = num //5
if num == 1:
return True
else:
return False
count = 0
num = 1
while True:
if isUglyNumber(num):
count += 1
if count == index:
return num
num += 1
第二种方法分析:
我们可以保存已经找到的丑数,然后 用空间环时间 来 找出丑数。
如何用空间换时间?
我们找一种,只需要计算丑数的办法,根据上面丑数的定义,我们可以知道,丑数应该是另一个丑数 乘以 2,3,或者5 的结果(1除外)。因此我们 可以创建一个 列表,里面的数字是排好序的 丑数,每个丑数都是前面的丑数乘以2,3,或者5得到的。
那么我们就可以在一个列表中,给它第一个 丑数的值,然后根据 它 得到剩下的 丑数的值,第一个丑数为1,那么我们在这个列表的起始位置 设置三个指针,这三个指针代表的值 分别为2,3,5.又由于这个列表中的所有的丑数 是有序的,从小到大排列的,那么我们在每次 给一个丑数 乘以 2,3,5 以后要与前面的丑数比较大小,然后在根据大小值 来放入列表中。由于一开始第一个丑数是1,那么 1 * 2 得到的是2,1*3 得到的是3,1 乘以5 得到的是5,那么三个数中比较大小,最小的是 1 乘以2,那么 肯定第一个先放置的是2,然后是 2 乘以2 和 1乘3,1乘5 比较大小,最小的是3 那么就放置 3,下一个 是 2 乘以3 是6,6 与 5 和4 比较大小 最小的是4,以此类推,那么现在的到的丑数的顺序就是1,2,3,4.。。。。。
class Solution(object):
def nthUglyNumber(self, index):
#首先判断 要找的 丑数 是不是第0个 或者是负数,如果是的话,那么就返回0
if index <= 0:
return 0
#然后判断要找的丑数 是不是第一个,如果是第一个,那么就返回1.
if index == 1:
return 1
#在丑数 这个列表中 给出第一个丑数是1
numbers = [1]
#在列表的 一开始 设置三个 指针,也就是 三个指针的 索引位置是0,
two, three, five = 0, 0, 0
#丑数的个数 起始为 1
count = 1
#循环 当丑数的个数不等于我们要找到 那第 index 个 丑数时,就循环,等于的时候就跳出循环。
while count != index :
#给列表中的 2,3,5 这三个指针所在位置的 丑数 分别 乘以2,3,5
n2, n3, n5 = numbers[two] * 2, numbers[three] * 3, numbers[five] * 5
#比较这三个丑数的大小
minValue = min(n2, n3, n5)
#在丑数列表中,把三个中最小的那个 放进去。
numbers.append(minValue)
#每放进去一个,丑数的数量就加1
count += 1
#这个是指针移位的,如果说我们比较出来的 三个数中最小的丑数是 2 指针的话,那么2 指针就往前移动一位
if minValue == n2:
two += 1
#如果是 3 那个指针的话,那么3 这个指针就移一位。
if minValue == n3:
three += 1
#如果是 5 那个指针的话,那么5这个指针就移一位。
if minValue == n5:
five += 1
#最后输出这个丑数列表中的 最后一位,那么就是我们的计数的丑数的个数 -1,就是最后一个丑数的索引值。
return numbers[count-1]