决策树和分类树
决策树和分类树
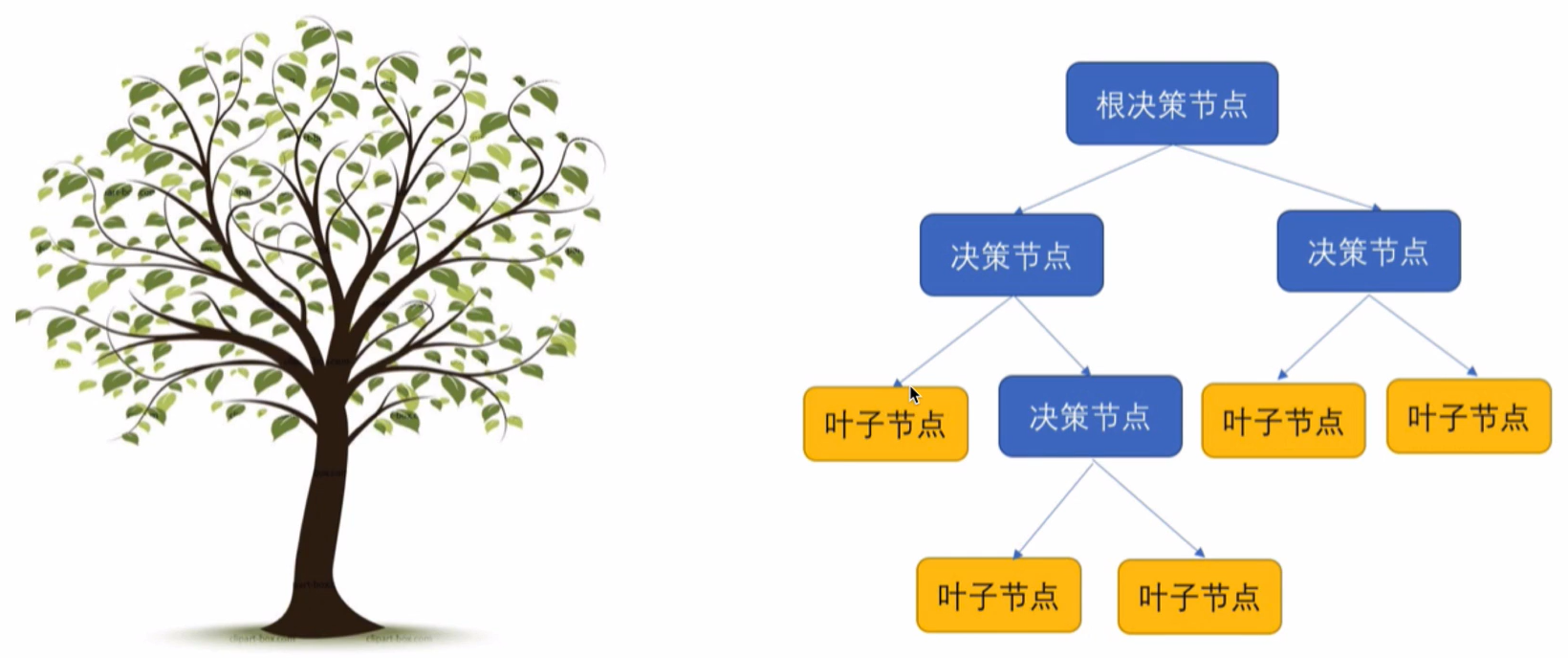
决策树的直观理解
分类树之信息熵
信息熵
信息熵是用阿里衡量信息不确定性的指标,不确定性是一个时间出现不同结果的可能性,计算方式如下所示: $$ H(X)=-\sum_{i=1}^{n} P(X=i) \log _{2} P(X=i) $$ 其中:P(X=i) 为随机变量X取值为i的概率。
下面以抛硬币为例,得到两个不同的熵值
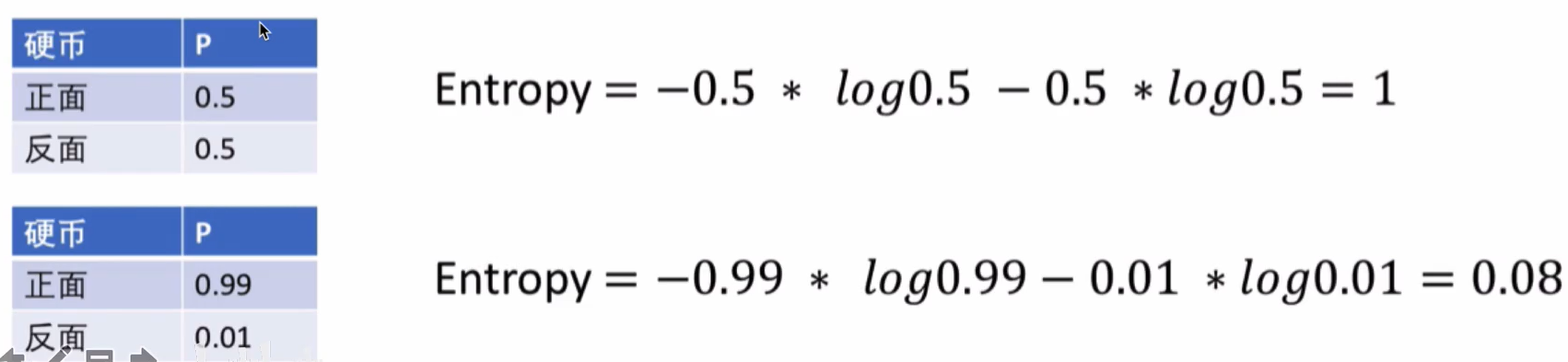
从上可知,不确定性越大的时候,得到的熵也越高,如百分50概率的时候,我们得到熵为1,而当正面为0.99的时候,熵值为0.08
条件熵
在给定随机变量Y的条件下,随机变量X的不确定性,也就是对条件概率求信息熵 $$ H(X | Y=v)=-\sum_{i=1}^{n} P(X=i | Y=v) \log _{2} P(X=i | Y=v) $$
信息增益
熵 减去 条件熵 得到的就是信息增益,代表了在一个条件下,信息不确定性减少的程度。
$$
I(X, Y)=H(X)-H(X | Y)
$$
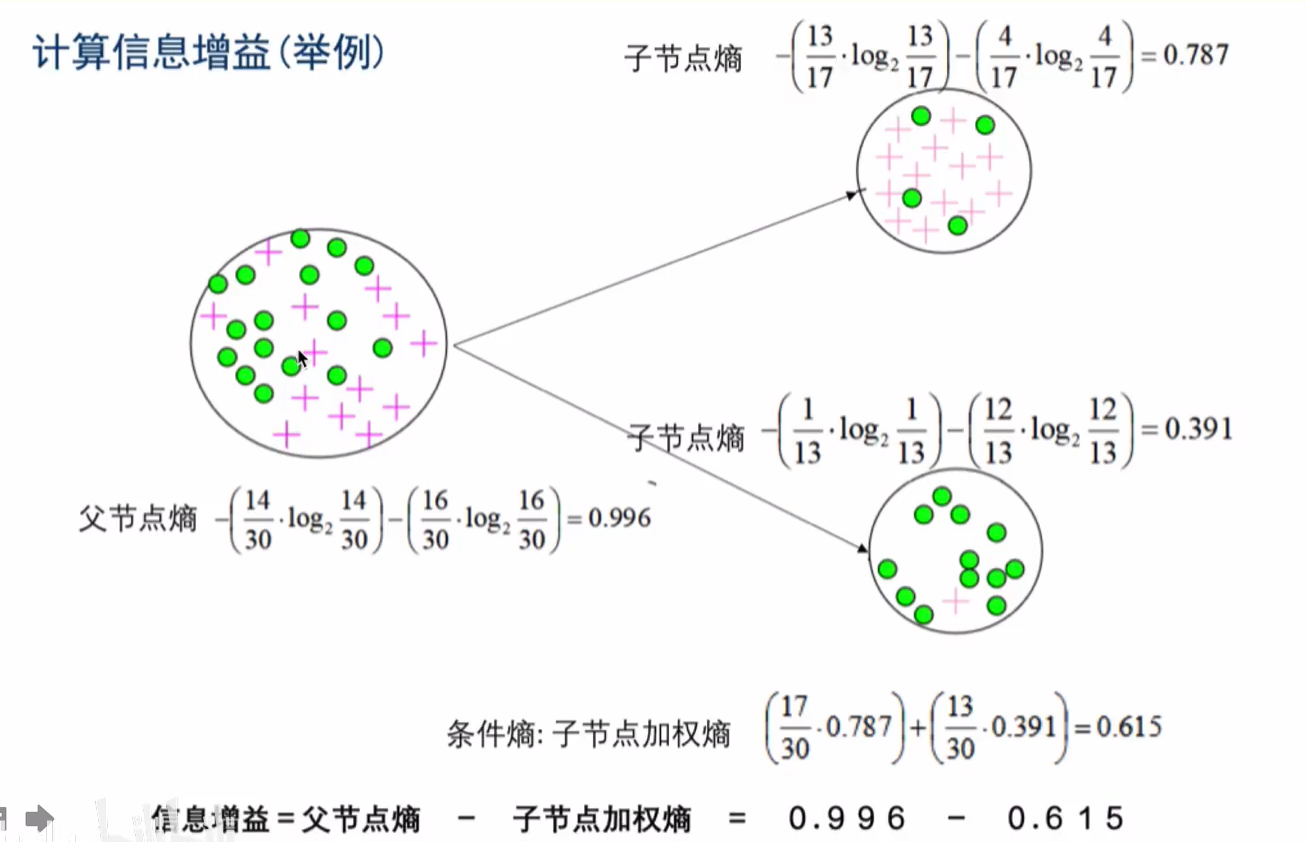
举例
假设高尔夫球场拥有不同天气下某个客户的打高尔夫球的历史记录如右图所示我们无法单纯的通过Yes和No的历史频率判断用户明天会不会打高尔夫因此我们需要借助天气信息减少不确定性
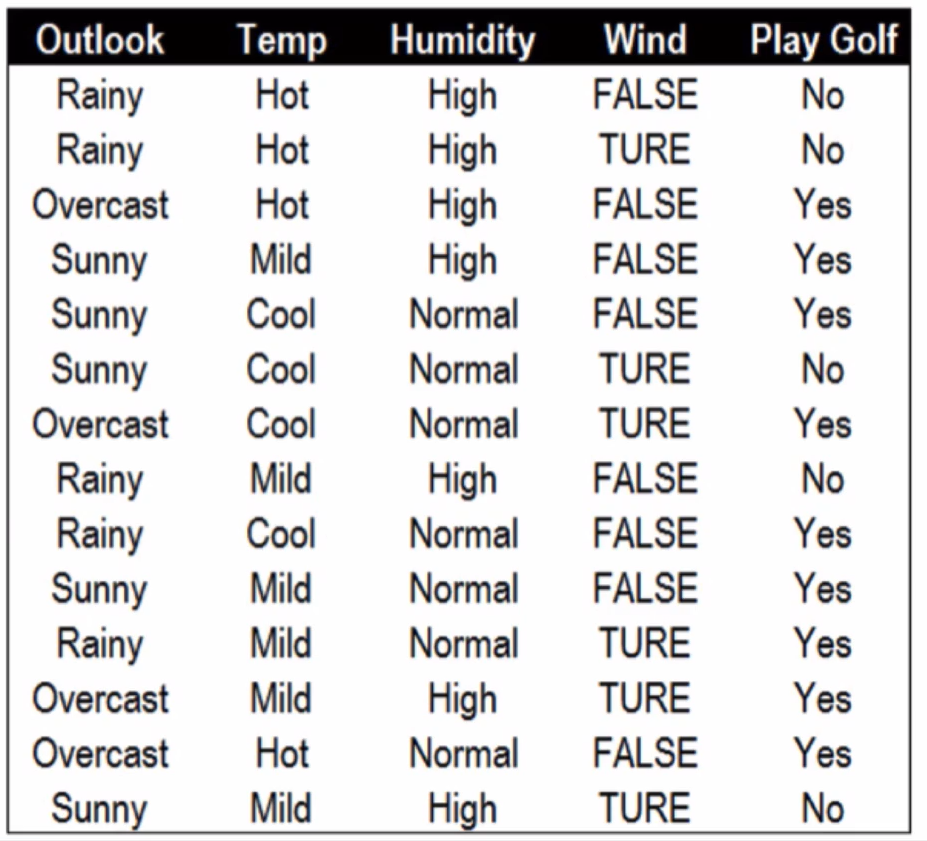
首先是构建根节点,我们先看下 Play Golf的熵:

在14条历史数据中,打球的概率为0.64,不打球的概率为0.36,熵值为0.94。接下来我们寻找睛朗与否,湿度,风力和温度四种状况与是否打高尔夫相关性最高的一个,进行决策树的构建。
晴朗程度Outlook的条件熵与信息增益:
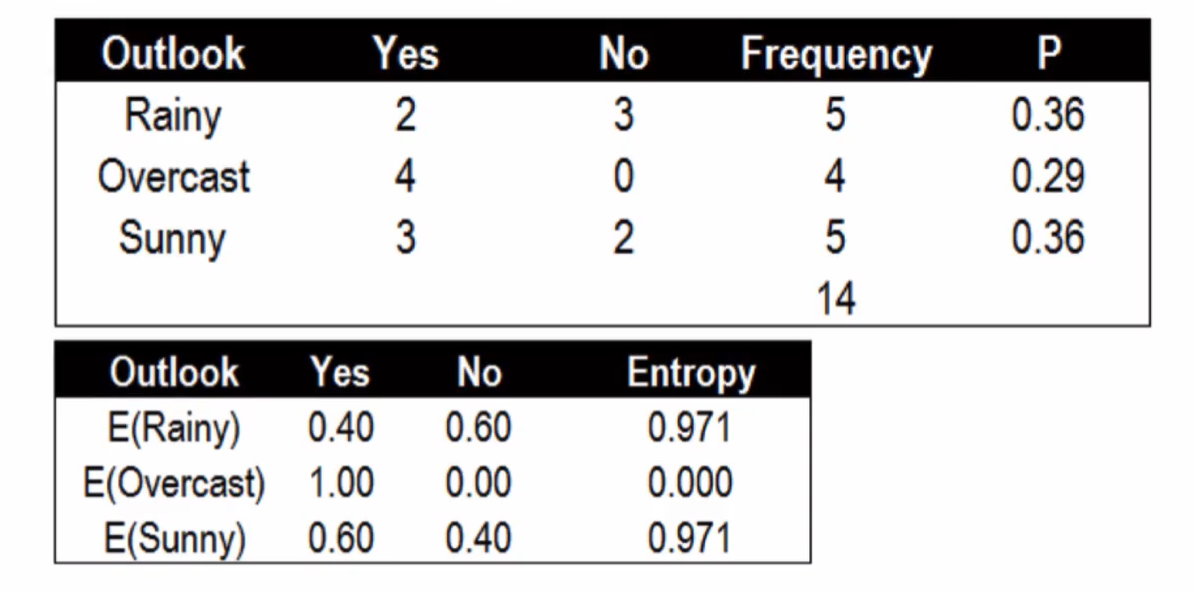
使用Outlook的条件熵 0.36 * 0.971 + 0.29 * 0 + 0.36 * 0.971 = 0.69
信息增益:0.940 - 0.69 = 0.25 (最佳分割特征)
温度Temp的条件熵与信息增益
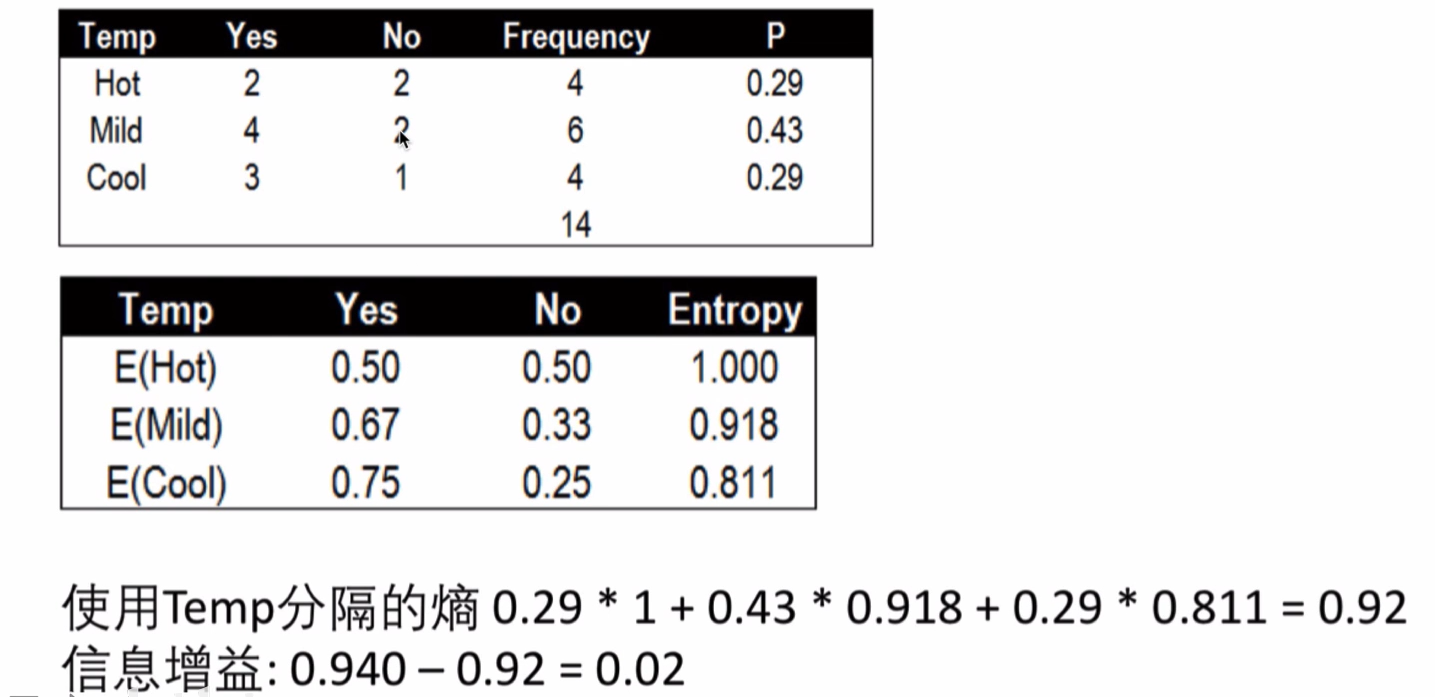
风力Wind的条件熵与信息增益
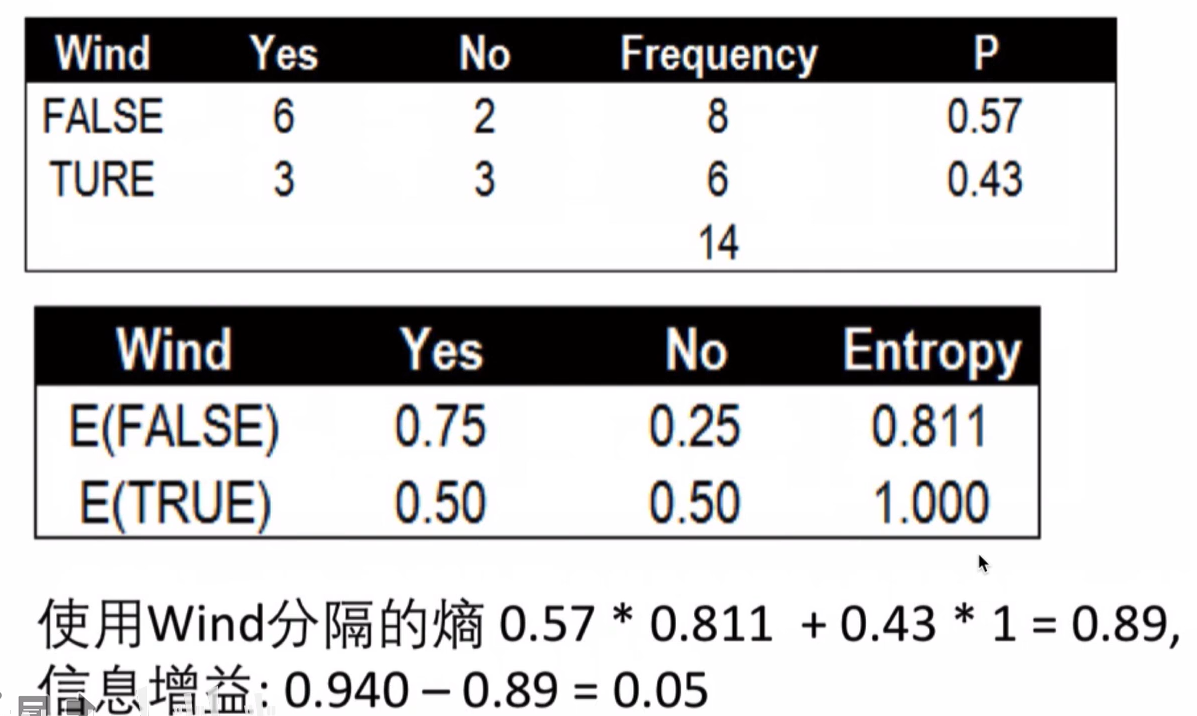
总结
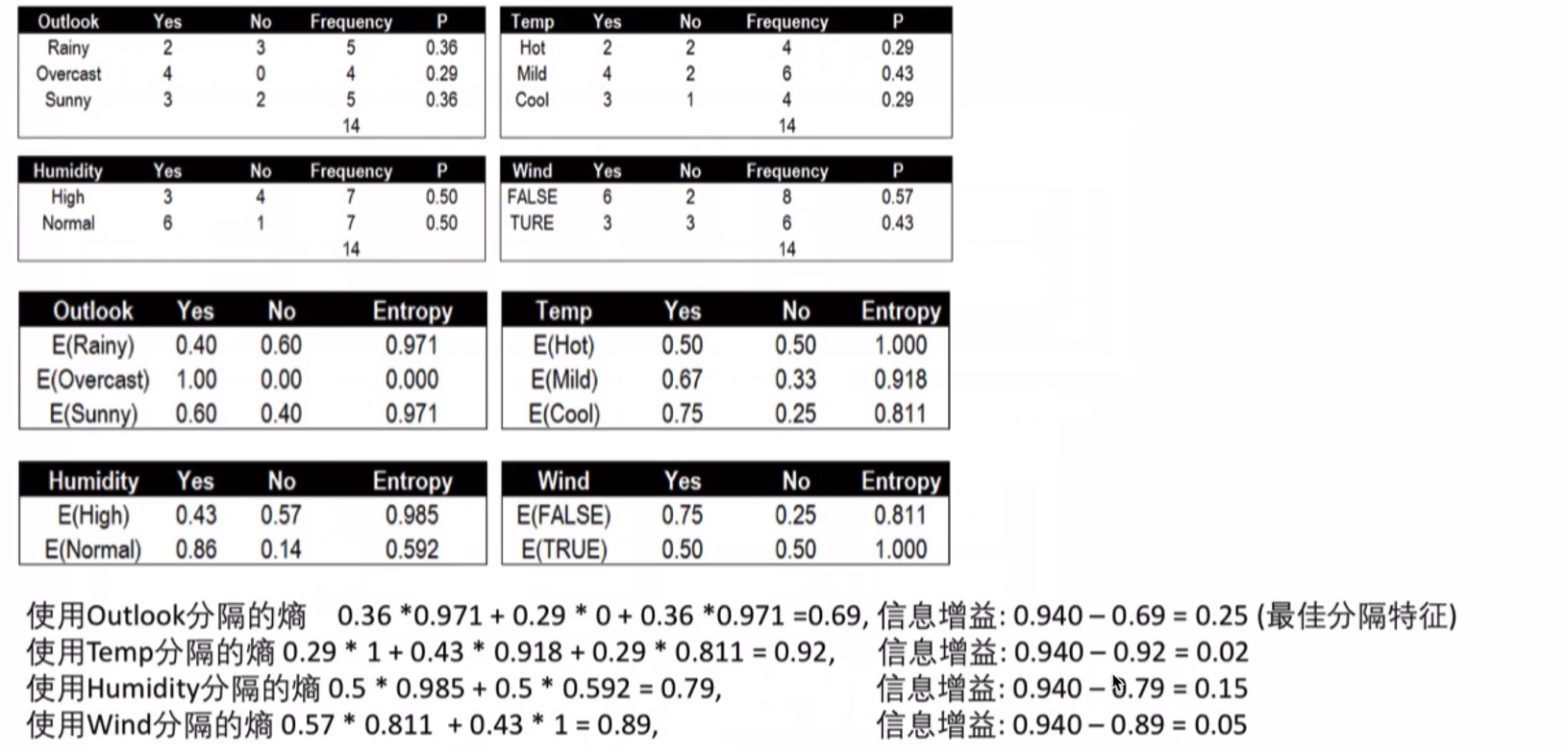
这个时候,我们需要选择信息增益最大的,也就是 Outlook作为 最佳分隔特征
构建步骤
根节点分隔结果
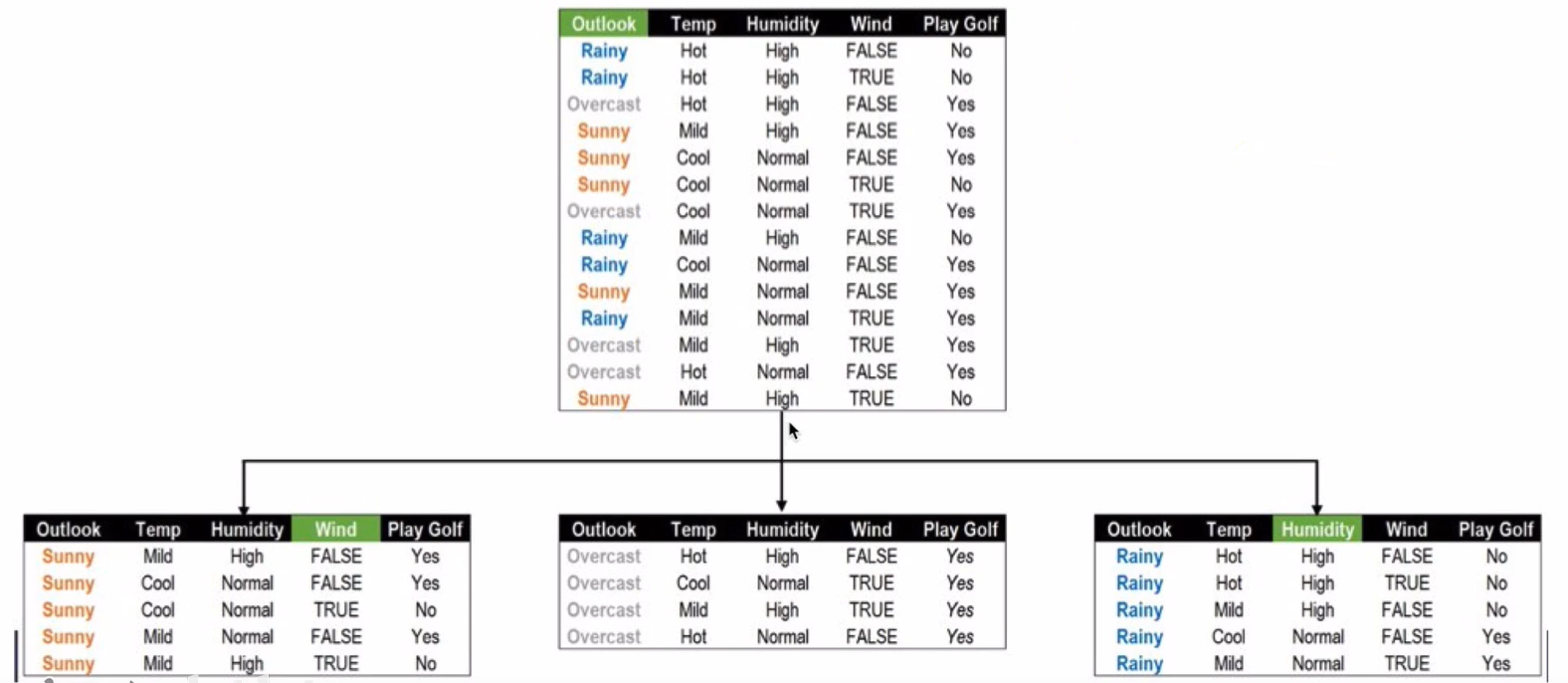
根节点和OverCast节点分隔结果:
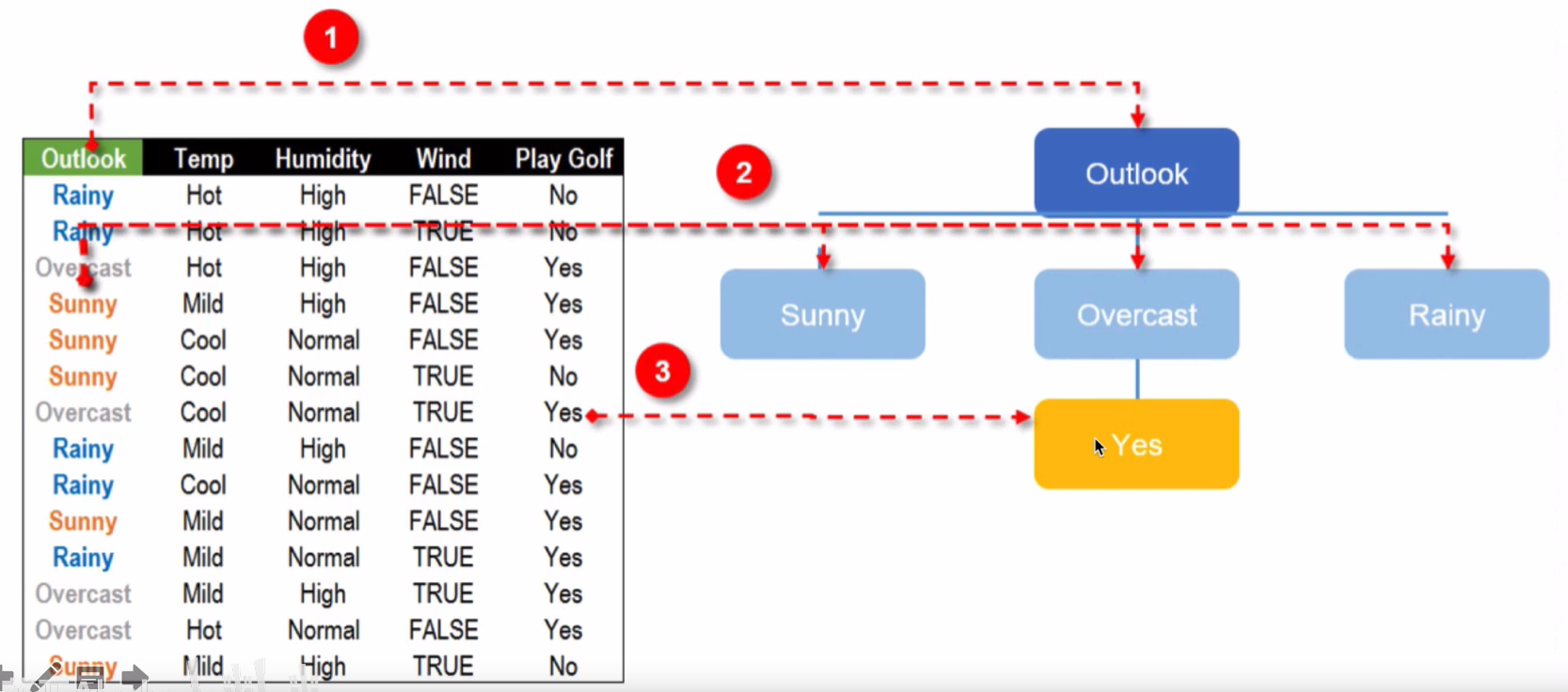
Sunny节点分隔结果:
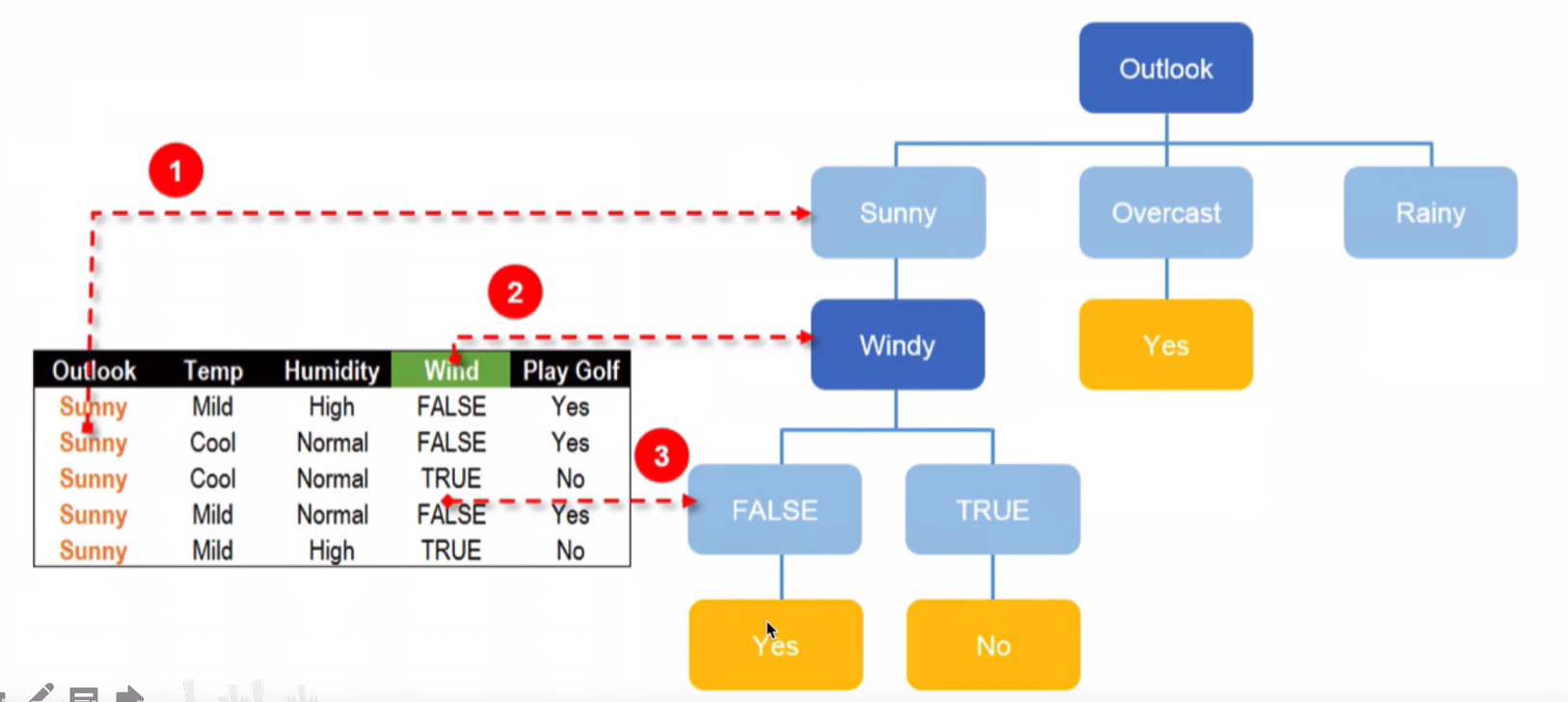
Rainy节点分隔结果:
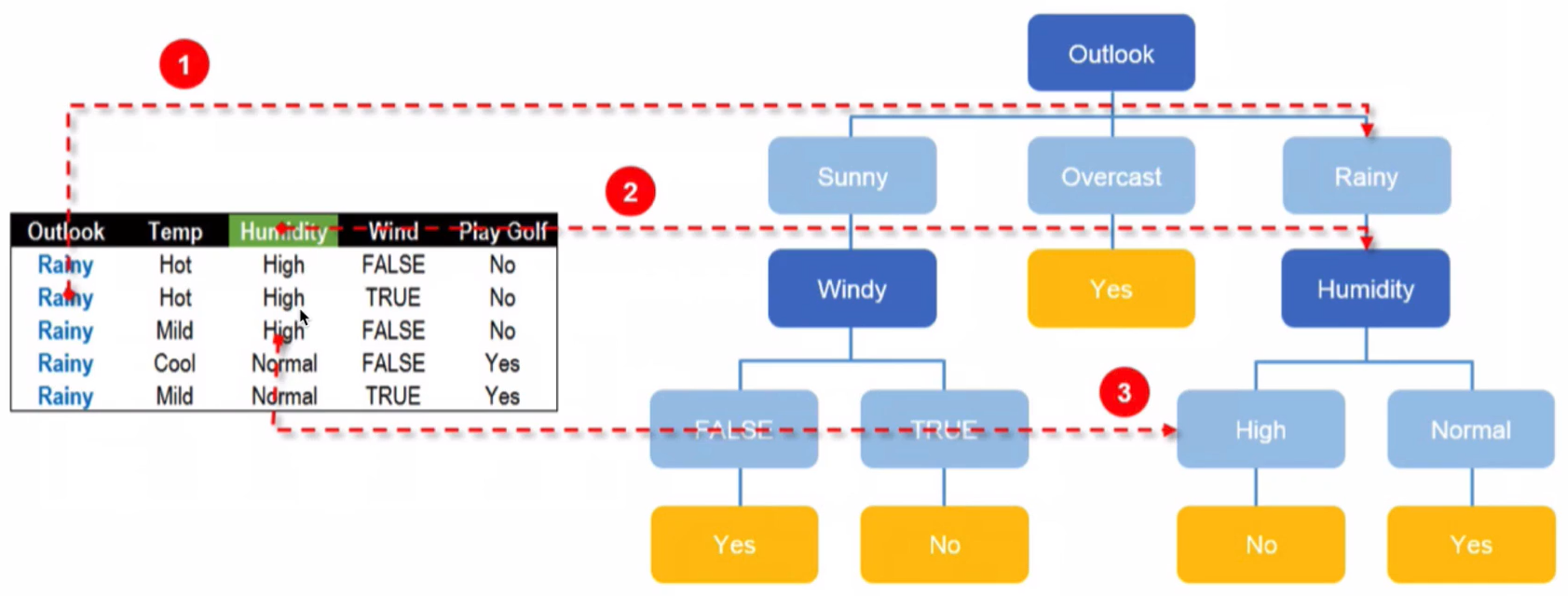
最终结果
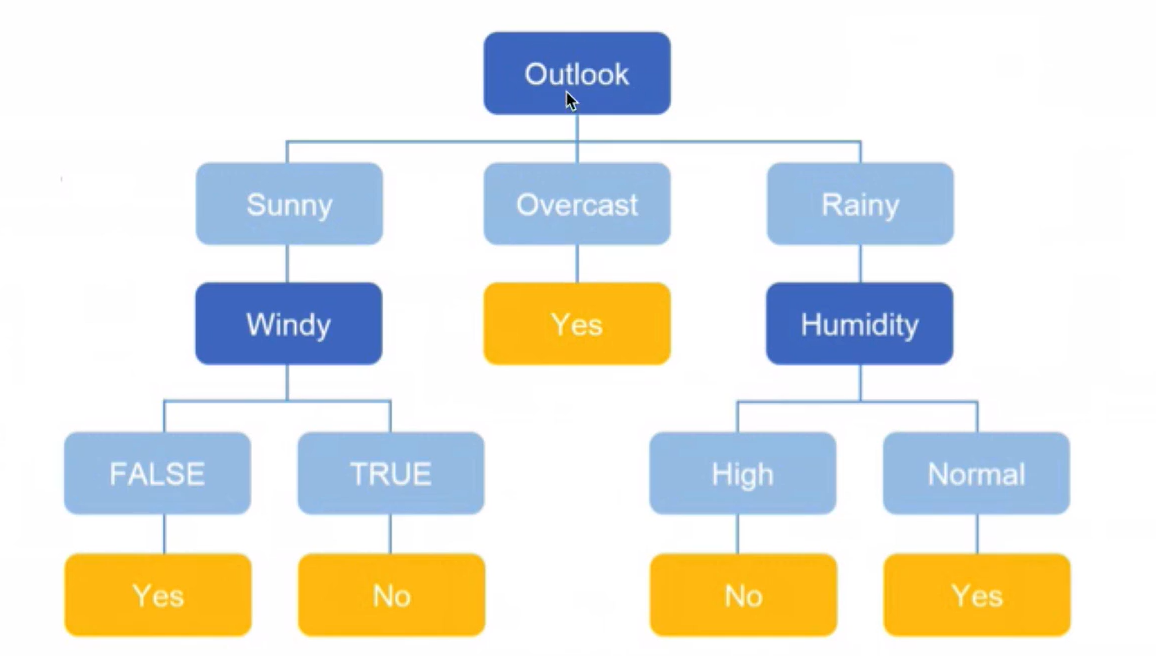
使用决策树进行预测
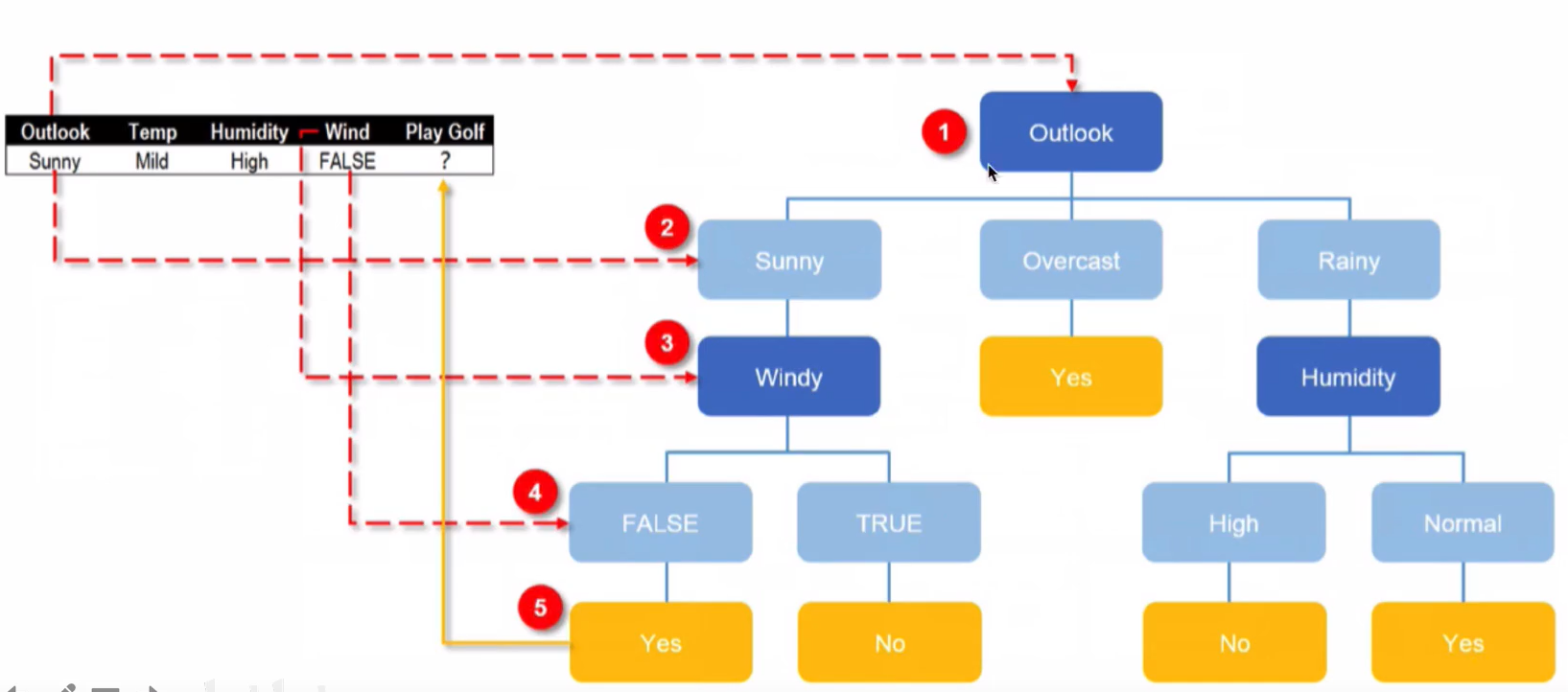
分类树之基尼指数
基尼指数(Gn不纯度)表示在样本集合中一个随机选中的样本被分错的概率
注意:Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。当集合中所有样本为个类时,基尼指数为0基尼指数的计算方法: $$ \operatorname{Gini}(\mathrm{p})=\sum{k=1}^{K} p{k}\left(1-p{k}\right)=1-\sum{k=1}^{K} p_{k}^{2} $$ 其中,pk表示选中的样本属于第K个类别的概率
案例
根据天气计算基尼指数
根据天气状况预测是否打高尔夫球,首先计算根节点的基尼指数
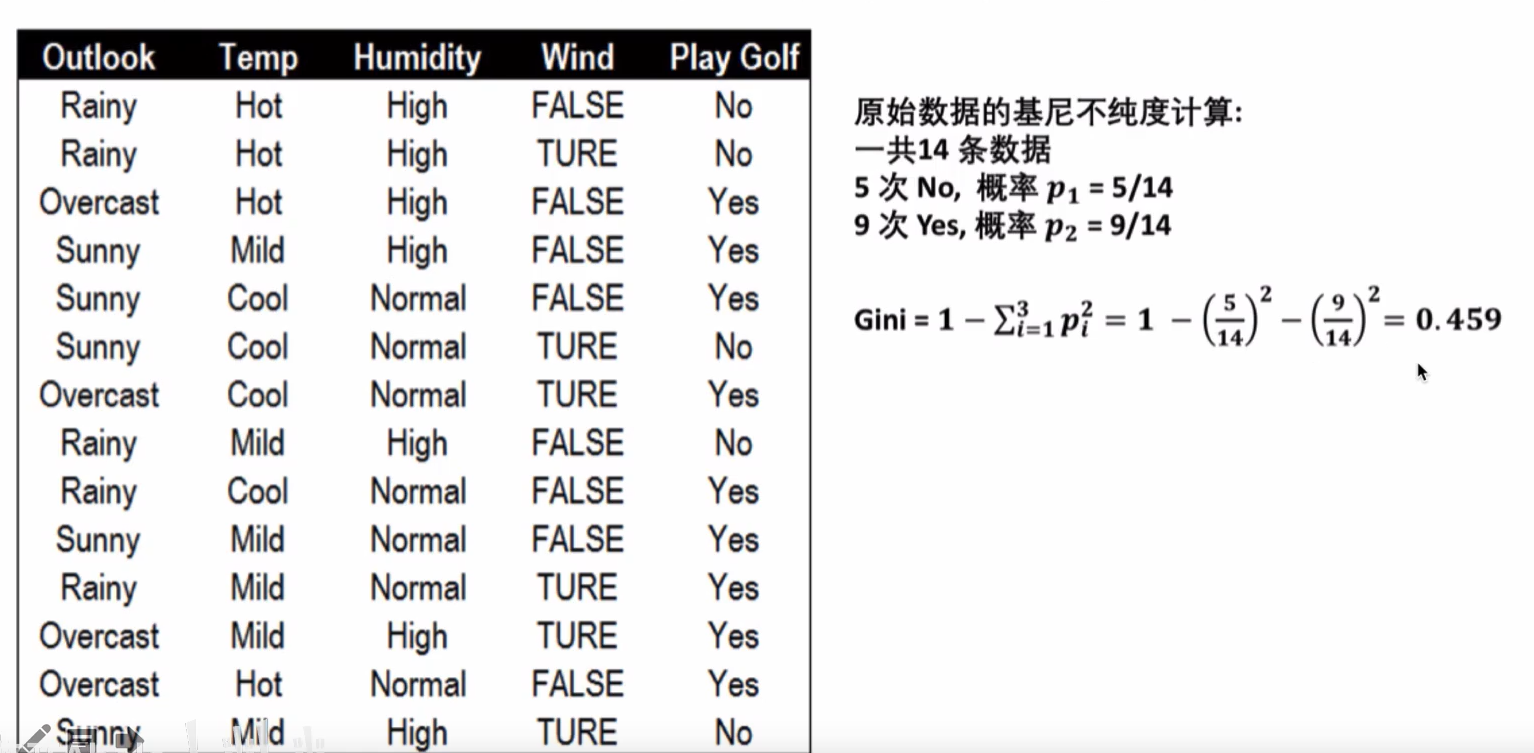
根据晴朗程度计算基尼指数
晴朗程度Outlook的基尼指数

根据温度的基尼指数
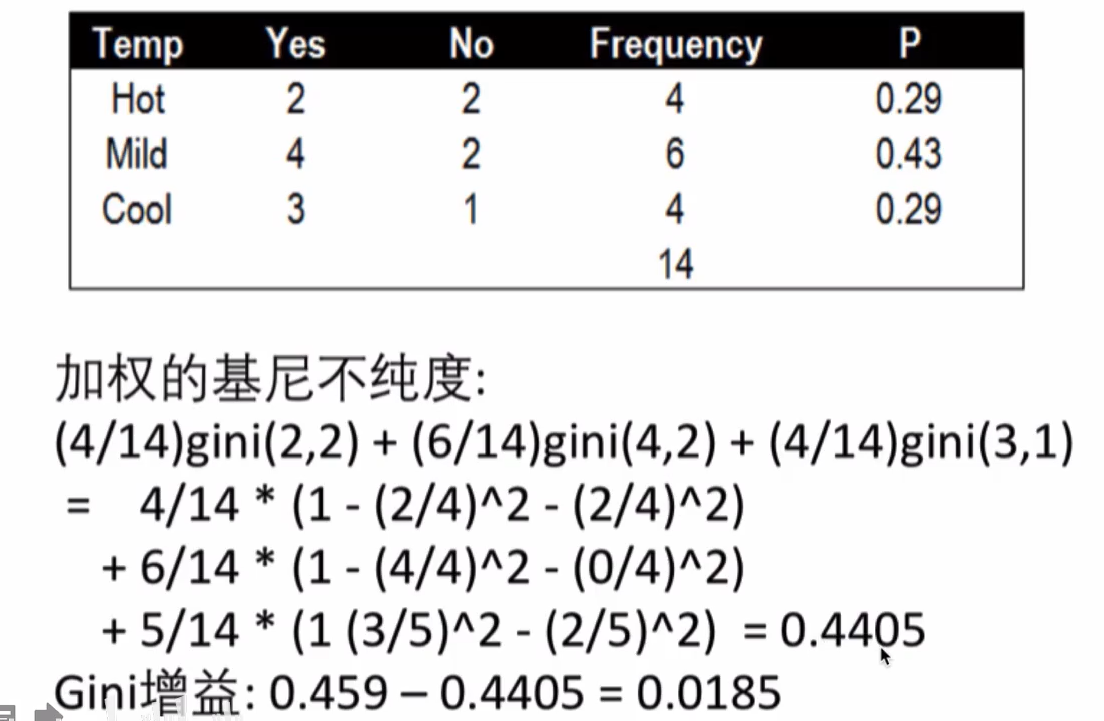
湿度的基尼指数

风力的基尼指数
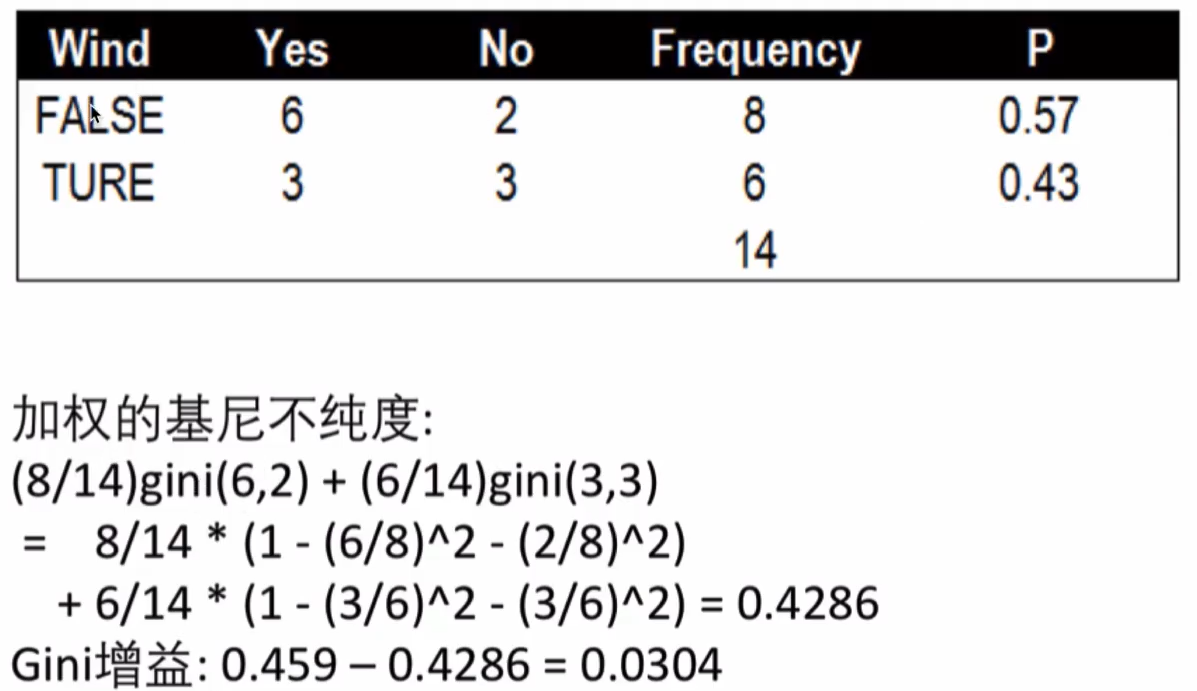
最佳分割点
使用基尼指数来分割的树叫CART树,CART树是二叉树,对于一个具有多个取值(超过2个)的特征,需要计算以每一个取值作为划分点,对样本D划分之后子集的纯度Gn(DAi),然后从所有的可能划分的Gin(DA)中找出Gin指数最小的划分,这个划分的划分点,便是使用特征A对样本集合D进行划分的最佳划分点。
- 使用 Outlook分隔的Gini增益:0.117(最佳分隔特征)
- 使用Temp分隔的Gin增益:0.0185
- 使用 Humidity.分隔的Gin增益:00916
- 使用Wnd分隔的Gin增益:0.0304
Outlook是最优的分割特征,揭下来计算 rainy, overcast和suny的基尼指数,选择最小的作为分割节点即可
回归树
回归树( regression tree),就是用决策树模型做回归问题,每片叶子都输出一个预测值。预测值一般是叶子节点所含训练集元素输出的均值
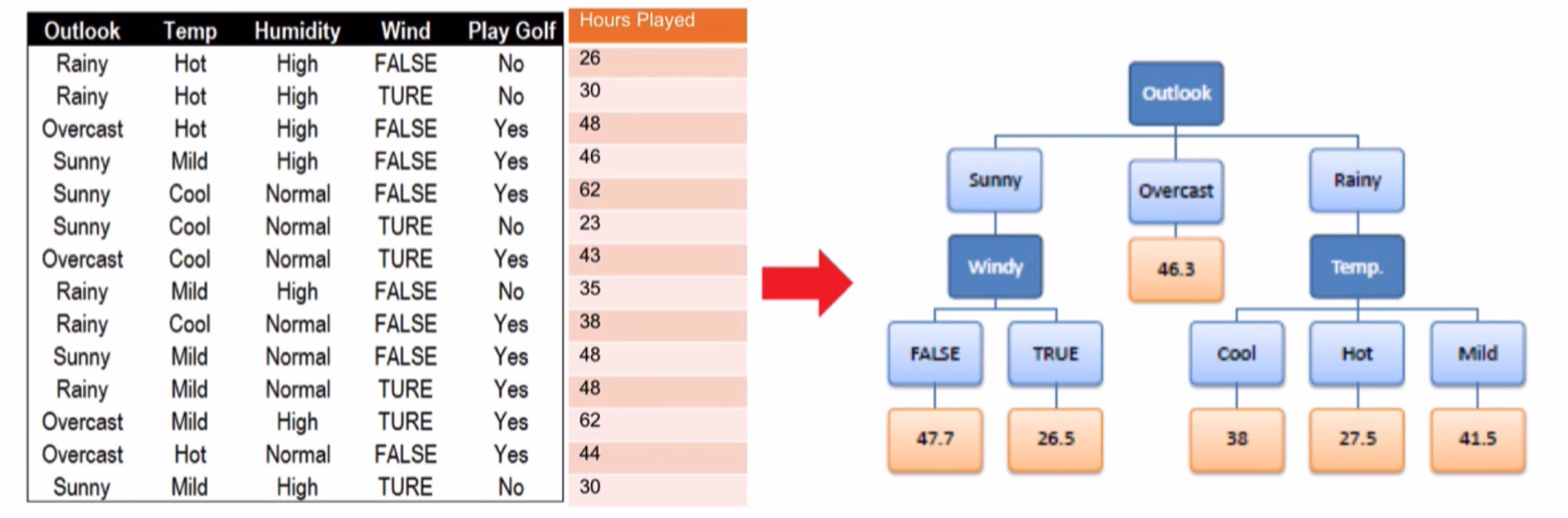
回归树的分支标准:标准方差( Standard deviation)。回归树使用某特征将原集合分为多个子集,用标准方差衡量子集中的元素是否相近越小表示越相近。首先计算根节点的标准方差

分支
使用标准方差来确定分支,以计算 Outlook分支后的标准差为例:
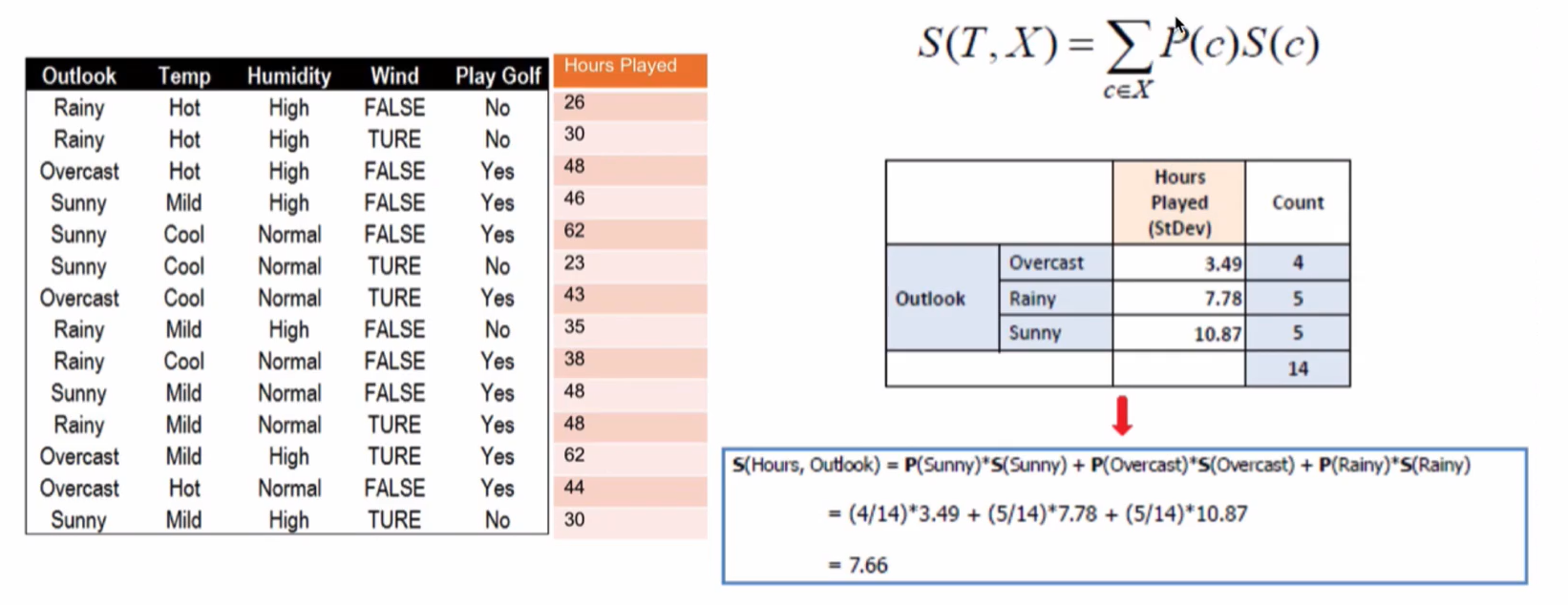
同理可计算其他特征的标准方差,并得到方差的减小值:
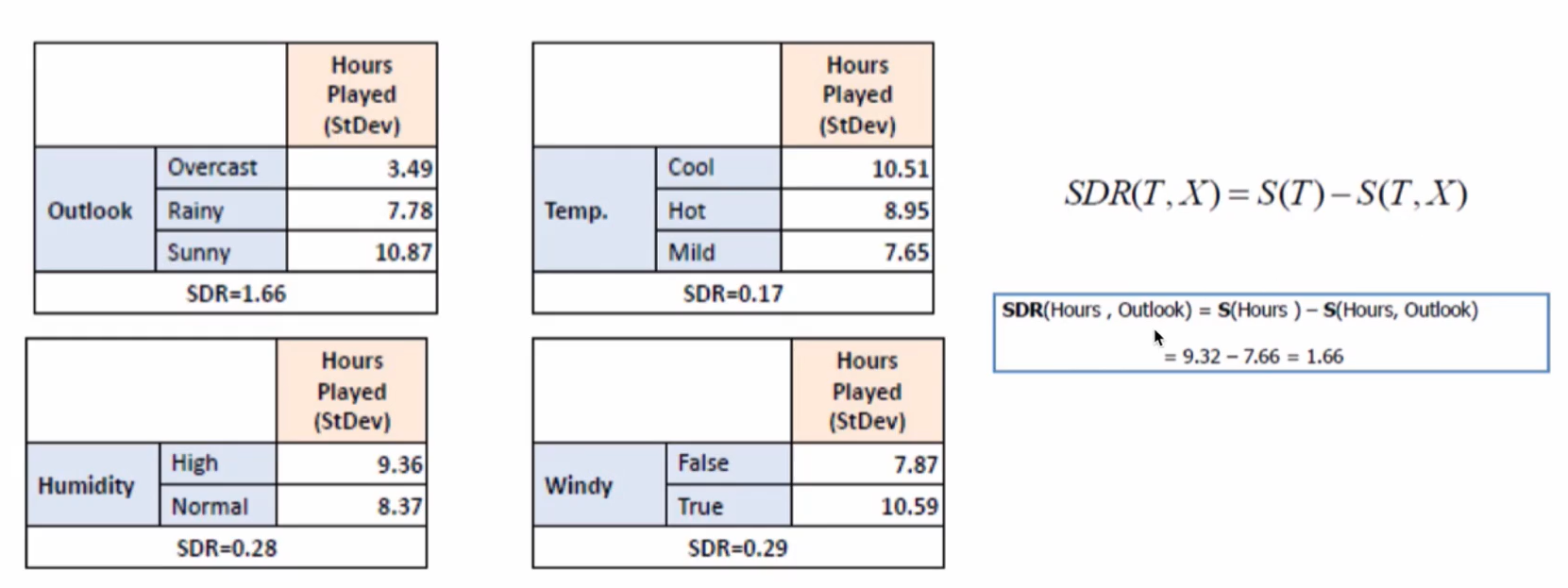
标准差降低最多的特征是 Outlook,利用其进行分支
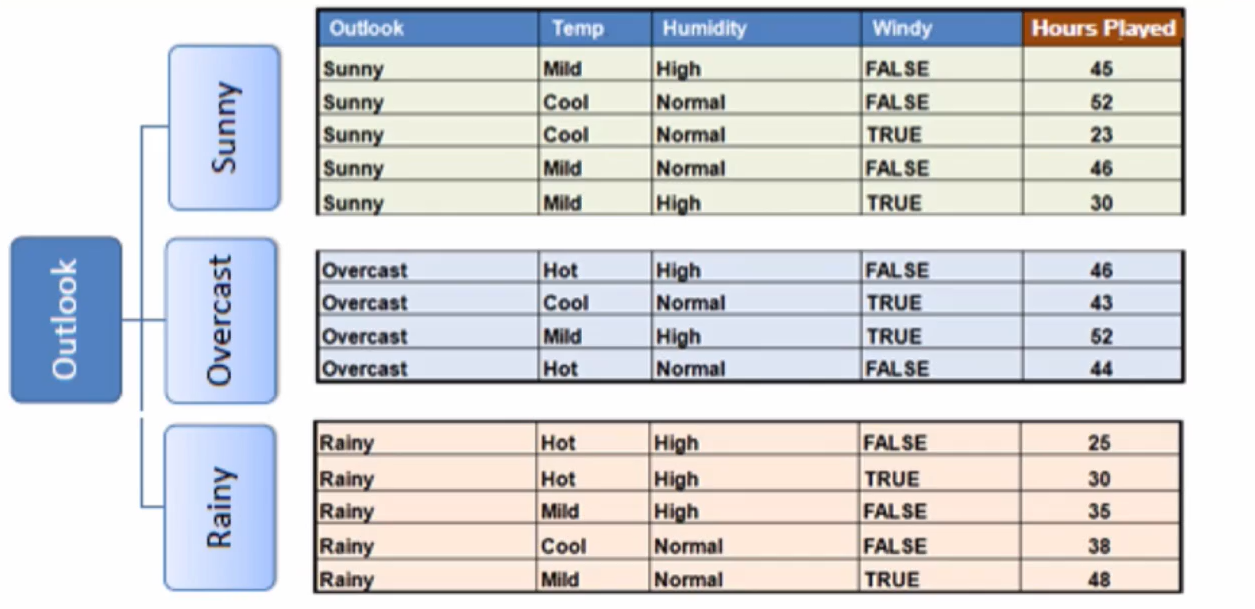
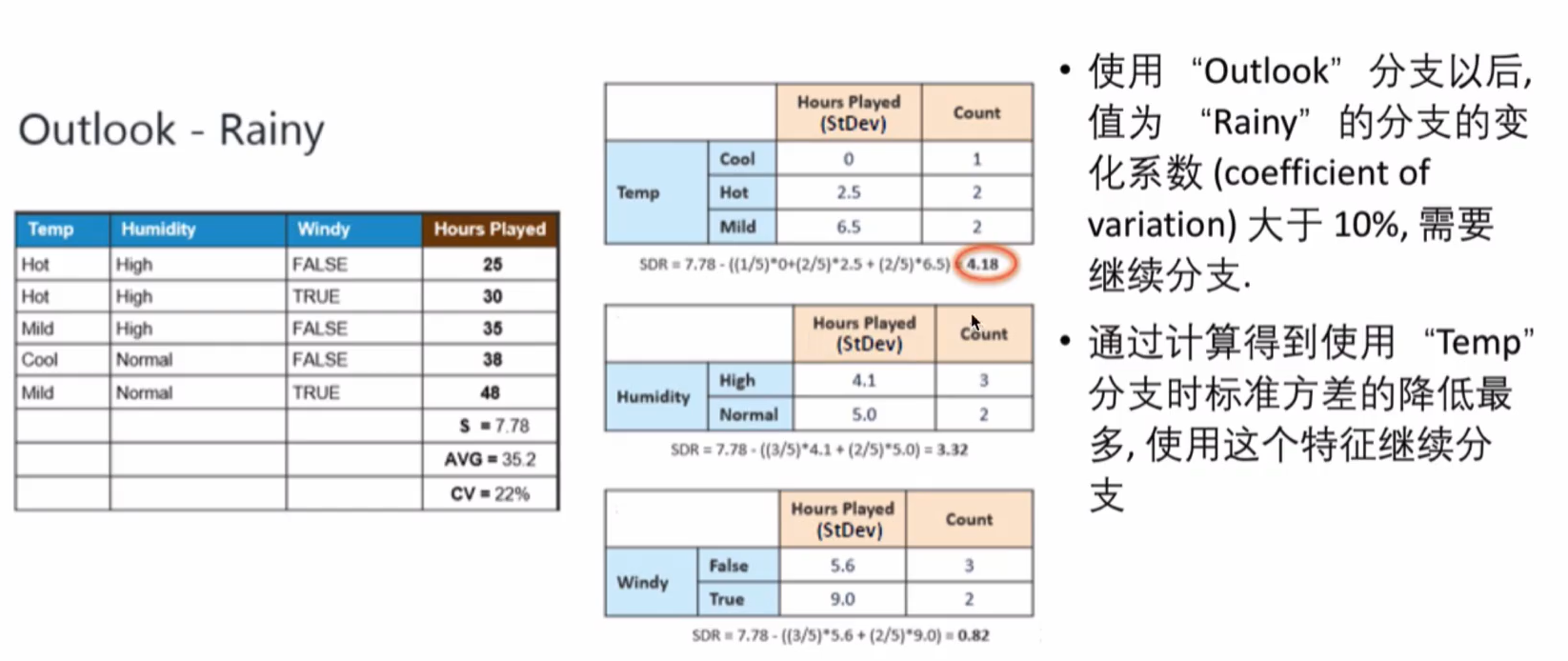
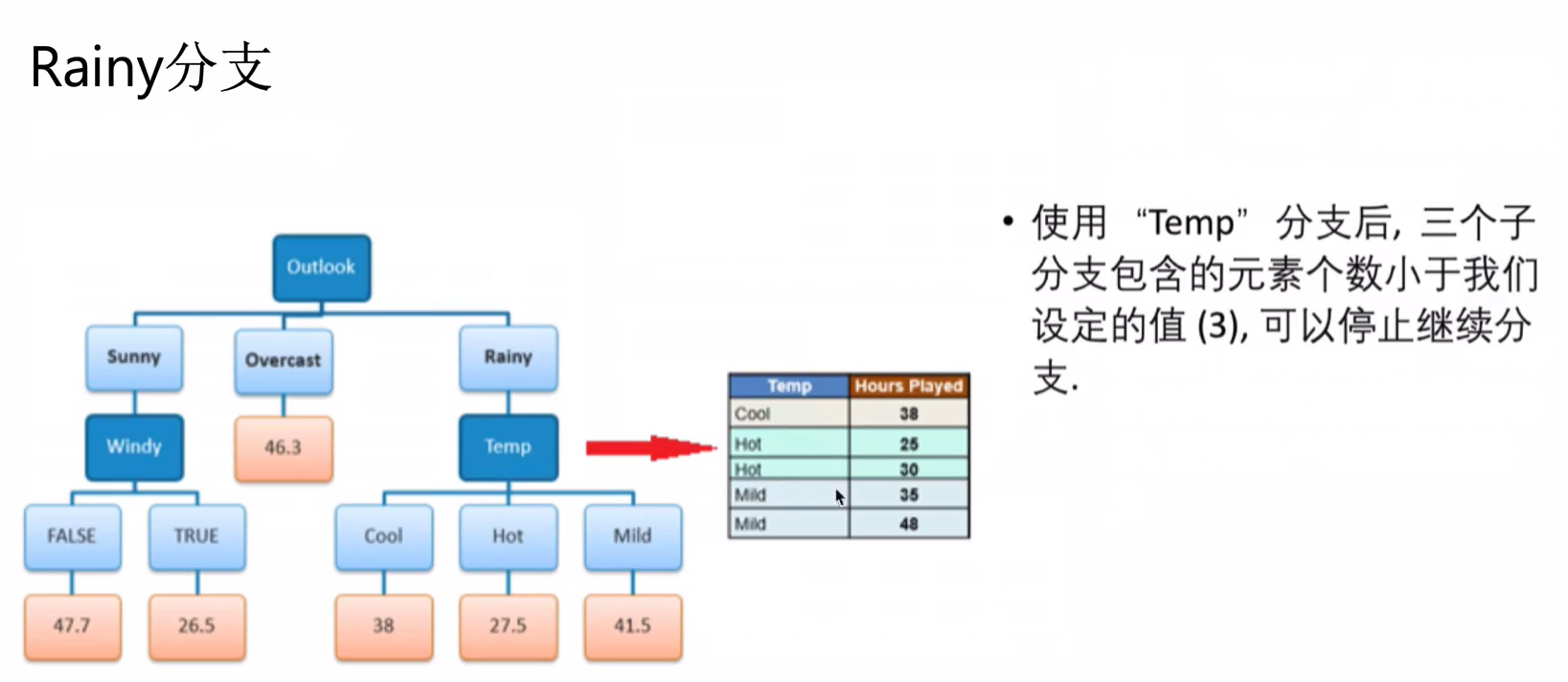
接下来,重复这个过程,使用标准方差降低最多的特征进行分支直到满足某个停止条件,如:1.当某个分支的变化系数小于某个值(10%),2.当前节点包含的元素个数小于某个值(3)
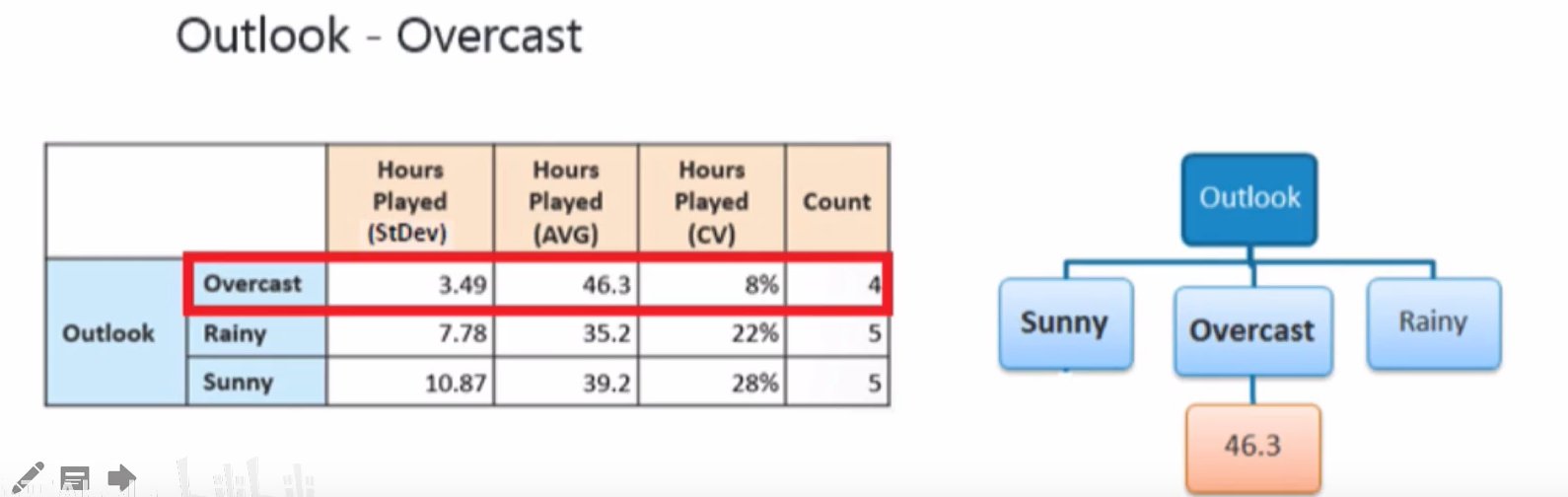
使用“ outlook“分支以后,值为“ Overcast”的分支的变化系数( coefficient of variation)太小(8%)小于我们设置的最小值(10%,停止继续在“ Overcast 对应的分支上继续分支,生成亠个叶子节点
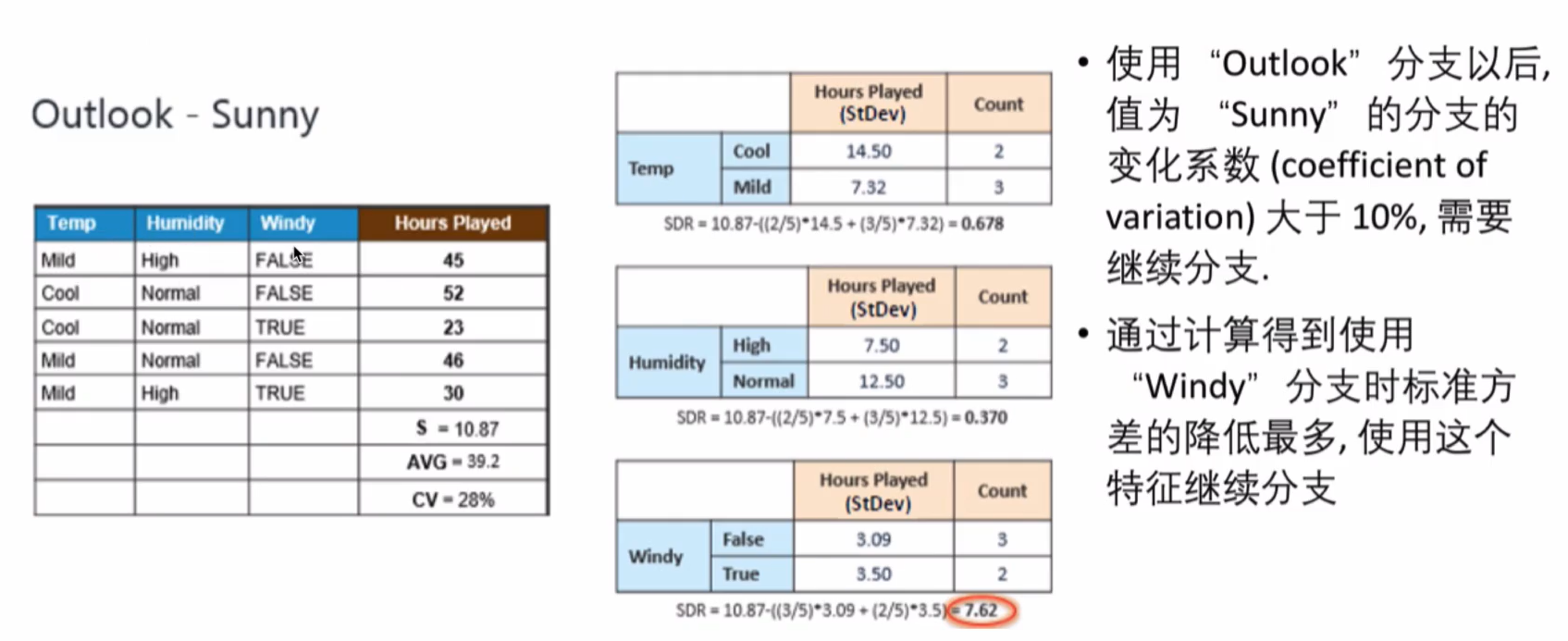
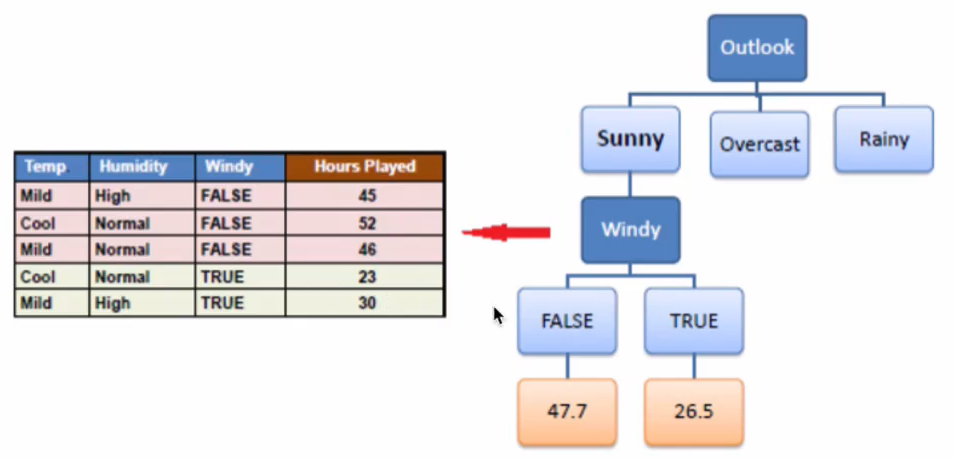
Sunny分支
使用“ Windy”分支后,两个子分支包含的元素个数小于我们设定的值(3),可以停止继续分支